题目内容
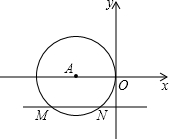 如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(-8,-4),则点N的坐标为
如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(-8,-4),则点N的坐标为考点:切线的性质,坐标与图形性质
专题:计算题
分析:作AB⊥MN于B,连结AM,如图,设⊙A的半径为r,先根据切线的性质得OA=r,则点A的坐标为(-r,0),再利用垂径定理得BM=BN,利用MN∥x轴,M(-8,-4),得到B点坐标为(-r,-4),然后在Rt△ABM中,根据勾股定理得42+(8-r)2=r2,解得r=5,则BM=BN=3,易得N点坐标为(-2,-4).
解答:解:作AB⊥MN于B,连结AM,如图,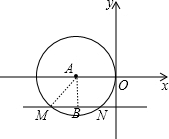 设⊙A的半径为r,
设⊙A的半径为r,
∵⊙A与y轴相切于原点O,
∴OA=r,
∴点A的坐标为(-r,0),
∵AB⊥MN,
∴BM=BN,
∵MN∥x轴,M(-8,-4),
∴B点坐标为(-r,-4),
在Rt△ABM中,AB=4,AM=r,BM=8-r,
∵AB2+BM2=AM2,
∴42+(8-r)2=r2,解得r=5,
∴BM=3,
∴BN=3,
∴N点坐标为(-2,-4).
故答案为(-2,-4).
 设⊙A的半径为r,
设⊙A的半径为r,∵⊙A与y轴相切于原点O,
∴OA=r,
∴点A的坐标为(-r,0),
∵AB⊥MN,
∴BM=BN,
∵MN∥x轴,M(-8,-4),
∴B点坐标为(-r,-4),
在Rt△ABM中,AB=4,AM=r,BM=8-r,
∵AB2+BM2=AM2,
∴42+(8-r)2=r2,解得r=5,
∴BM=3,
∴BN=3,
∴N点坐标为(-2,-4).
故答案为(-2,-4).
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了坐标与图形性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,∠A=30°,斜边AB=2,求:
如图,在Rt△ABC中,∠C=90°,∠A=30°,斜边AB=2,求: 如图所示,线段AD与BC相交,∠ADC与∠ABC的角平分线相交于O,若∠A=32°,∠C=48°,求∠O的度数.
如图所示,线段AD与BC相交,∠ADC与∠ABC的角平分线相交于O,若∠A=32°,∠C=48°,求∠O的度数.