题目内容
 如图所示,线段AD与BC相交,∠ADC与∠ABC的角平分线相交于O,若∠A=32°,∠C=48°,求∠O的度数.
如图所示,线段AD与BC相交,∠ADC与∠ABC的角平分线相交于O,若∠A=32°,∠C=48°,求∠O的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:先根据三角形内角和定理得出∠CDG与∠ABG的关系,再根据三角形外角的性质即可得出结论.
解答: 解:∵△ADG与△ABG中,∠CGD=∠AGB,∠A=32°,∠C=48°,
解:∵△ADG与△ABG中,∠CGD=∠AGB,∠A=32°,∠C=48°,
∴∠C-∠A=48°-32°=16°,
∴∠ADG=∠ABG-16°,
∴设∠ABG=x,则∠ADC=x-16°,
∵∠ADC与∠ABC的角平分线相交于O,
∴∠CDE=
∠ADC=
x-8°,∠OBC=
∠ABG=
x,
∵∠DEG是△CDE与△OBE的外角,
∴∠C+∠CED=∠O+∠OBC,即48°+
x-8°=∠O+∠
x,解得∠O=40°.
 解:∵△ADG与△ABG中,∠CGD=∠AGB,∠A=32°,∠C=48°,
解:∵△ADG与△ABG中,∠CGD=∠AGB,∠A=32°,∠C=48°,∴∠C-∠A=48°-32°=16°,
∴∠ADG=∠ABG-16°,
∴设∠ABG=x,则∠ADC=x-16°,
∵∠ADC与∠ABC的角平分线相交于O,
∴∠CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠DEG是△CDE与△OBE的外角,
∴∠C+∠CED=∠O+∠OBC,即48°+
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
比x的相反数小2的数是( )
| A、-x+2 | B、-x-2 |
| C、-(x-2) | D、x-2 |
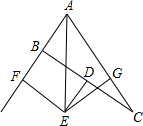 已知,AE平分∠FAC,EF⊥AF,∠AGE=90°,DE是BC垂直平分线,求证:BF=CG.
已知,AE平分∠FAC,EF⊥AF,∠AGE=90°,DE是BC垂直平分线,求证:BF=CG.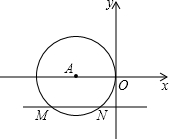 如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(-8,-4),则点N的坐标为
如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(-8,-4),则点N的坐标为 如图,已知在四边形ABCD中,AB=CD,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.
如图,已知在四边形ABCD中,AB=CD,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.