题目内容
17.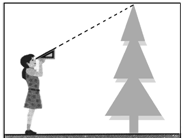 小莉站在离一棵树水平距离为2米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为($\frac{2\sqrt{3}}{3}$+1.5)米.(结果保留根号)
小莉站在离一棵树水平距离为2米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为($\frac{2\sqrt{3}}{3}$+1.5)米.(结果保留根号)
分析 过小莉的视点作树的垂线,通过构建直角三角形来求这棵树的高度.
解答  解:如图所示:过A作CD的垂线,设垂足为E点,
解:如图所示:过A作CD的垂线,设垂足为E点,
则AE=BC=2米,AB=CE=1.5米.
Rt△ADE中,AE=2米,∠DAE=30°,
∴DE=AE•tan30°=$\frac{2\sqrt{3}}{3}$(米),
∴CD=CE+DE=($\frac{2\sqrt{3}}{3}$+1.5)米.
故答案为:($\frac{{2\sqrt{3}}}{3}+1.5$)米.
点评 此题考查了仰角的定义、通过解直角三角形解决实际问题的能力.构造直角三角形是解决问题的关键.

练习册系列答案
相关题目
9.下列命题是正确的有( )
| A. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 | |
| B. | 三角形的内心到三角形各顶点的距离都相等 | |
| C. | 过同一平面内的任意三点有且仅有一个圆 | |
| D. | 半径相等的两个半圆是等弧 |
6.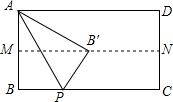 如图,点M、N分别是矩形ABCD的边AB和CD的中点,P是BC上的一点,△APB沿AP翻折后,点B恰好落在MN上,则∠APB=( )
如图,点M、N分别是矩形ABCD的边AB和CD的中点,P是BC上的一点,△APB沿AP翻折后,点B恰好落在MN上,则∠APB=( )
 如图,点M、N分别是矩形ABCD的边AB和CD的中点,P是BC上的一点,△APB沿AP翻折后,点B恰好落在MN上,则∠APB=( )
如图,点M、N分别是矩形ABCD的边AB和CD的中点,P是BC上的一点,△APB沿AP翻折后,点B恰好落在MN上,则∠APB=( )| A. | 30° | B. | 45° | C. | 60° | D. | 无法确定 |
 已知a,b,c在数轴上对应的点的位置如图所示:化简:|b+c|+|a+c|-|b-a|-|a+b+c|.
已知a,b,c在数轴上对应的点的位置如图所示:化简:|b+c|+|a+c|-|b-a|-|a+b+c|.