题目内容
16. 在平行四边形ABCD中,P为对角线BD上任意一点,连接PA、PC,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1=S2;②S1+S2=S3;③S1+S3=S2+S4;④若S1•S3=S2•S4,其中正确结论的序号是③.(在横线上填上你认为所有正确答案的序号)
在平行四边形ABCD中,P为对角线BD上任意一点,连接PA、PC,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1=S2;②S1+S2=S3;③S1+S3=S2+S4;④若S1•S3=S2•S4,其中正确结论的序号是③.(在横线上填上你认为所有正确答案的序号)
分析 根据平行四边形的对边相等可得AB=CD,AD=BC,设点P到AB、BC、CD、DA的距离分别为h1、h2、h3、h4,然后利用三角形的面积公式列式整理即可判断出③正确;根据三角形的面积公式即可判断①②④错误,即可得出结论.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
设点P到AB、BC、CD、DA的距离分别为h1、h2、h3、h4,
则S1=$\frac{1}{2}$ABh1,S2=$\frac{1}{2}$BCh2,S3=$\frac{1}{2}$CDh3,S4=$\frac{1}{2}$ADh4,
∵$\frac{1}{2}$ABh1+$\frac{1}{2}$CDh3=$\frac{1}{2}$AB•hAB,
$\frac{1}{2}$BCh2+$\frac{1}{2}$ADh4=$\frac{1}{2}$BC•hBC,
又∵S平行四边形ABCD=AB•hAB=BC•hBC,
∴S2+S4=S1+S3,
故③正确;①②④不正确;
故答案为:③.
点评 本题考查了平行四边形的性质,三角形的面积,以及平行四边形对角线上点的判定的应用,用平行四边形的面积表示出相对的两个三角形的面积的和是解题的关键,也是本题的难点.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
7.下列四个图形能围成棱柱的有几个( )
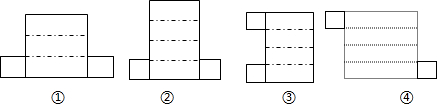

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
11. 下图中的几何体的左视图是( )
下图中的几何体的左视图是( )
 下图中的几何体的左视图是( )
下图中的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
16.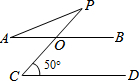 如图,AB∥CD,CP交AB于O,AO=PO,若∠C=50°,则∠A的度数为( )
如图,AB∥CD,CP交AB于O,AO=PO,若∠C=50°,则∠A的度数为( )
 如图,AB∥CD,CP交AB于O,AO=PO,若∠C=50°,则∠A的度数为( )
如图,AB∥CD,CP交AB于O,AO=PO,若∠C=50°,则∠A的度数为( )| A. | 25° | B. | 35° | C. | 15° | D. | 50° |
