题目内容
6. 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直接MN交BC于点M,交AD于点N.求证:四边形AMCN是菱形.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直接MN交BC于点M,交AD于点N.求证:四边形AMCN是菱形.
分析 由矩形ABCD与折叠的性质,易证得△CMN是等腰三角形,即CM=CN,即可证得AM=CM=CN=AN,即可得四边形AMCN是菱形.
解答 证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ANM=∠NMC,
由折叠的性质,可得:∠ANM=∠CNM,AM=CM,AN=CN,
∴∠NMC=∠CNM,
∴CM=CN,
∴AM=CM=CN=AN,
∴四边形AMCN为菱形.
点评 此题考查了矩形的性质、折叠的性质、菱形的判定,注意掌握菱形的判定方法,注意折叠中的对应关系.

练习册系列答案
相关题目
16.如果三角形的两边长分别为4和5,第三边的长是整数,而且是奇数,则第三边的长可以是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
 观察图,回答下列问题:
观察图,回答下列问题: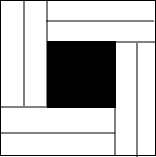 如图所示的正方形是由八块相同的长方形拼制而成的,且长与宽之比为4:1,中间留下一个边长为2mm的小正方形,你能求出长方形的长与宽吗?大正方形的面积是多少?
如图所示的正方形是由八块相同的长方形拼制而成的,且长与宽之比为4:1,中间留下一个边长为2mm的小正方形,你能求出长方形的长与宽吗?大正方形的面积是多少? 如图,点A为一次函数y=-x+5与反比例函数y=$\frac{2}{x}$图象的一个交点,AB⊥y轴于点B,AC⊥x轴于点C,则矩形ABOC的面积为多少?周长为多少?
如图,点A为一次函数y=-x+5与反比例函数y=$\frac{2}{x}$图象的一个交点,AB⊥y轴于点B,AC⊥x轴于点C,则矩形ABOC的面积为多少?周长为多少?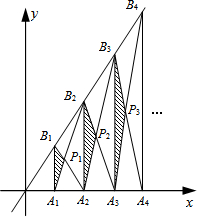 已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=2x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2 B3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn.若△A1B1P1,△A2B2P2,△A3B3P3,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn为$\frac{{n}^{2}}{2n+1}$.
已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=2x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2 B3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn.若△A1B1P1,△A2B2P2,△A3B3P3,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn为$\frac{{n}^{2}}{2n+1}$.