题目内容
定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段与线段的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点.
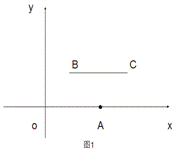
(1)根据上述定义,当m=2,n =2时,如图1,线段BC与线段OA的距离是_____,
=2时,如图1,线段BC与线段OA的距离是_____,
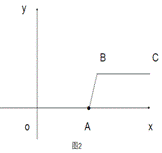
当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为______


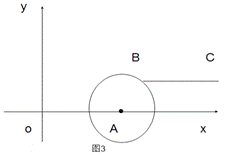

(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M.
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值,使以A、M、H为顶点的三角形与△AOD相似,若存在,求出m的值;若不存在,请说明理由.




(1)2;
 (2)
(2)
 (3)①16+4π②存在,m=1,m=3,m=
(3)①16+4π②存在,m=1,m=3,m=

【解析】解:(1)2;
 。
。
(2)∵点B落在圆心为A,半径为2的圆上,∴2≤m≤6。
当4≤m≤6时,根据定义, d=AB=2。
当2≤m<4时,如图,过点B作BE⊥OA于点E,

则根据定义,d=EB。





②存在。如图,
由A(4,0),D(0,2), 得
 。
。

又FM4=2,∴
 。
。
若△AOD∽△A H2M2,则
 ,即
,即
 ,
,
解得
 (不合题意,舍去)。此时m=
(不合题意,舍去)。此时m=
 。
。
若△AOD∽△M2H2 A,则
 ,即
,即
 ,
,
解得
 (不合题意,舍去)。
(不合题意,舍去)。


 阅读快车系列答案
阅读快车系列答案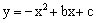 的顶点为D(﹣1,4),与
的顶点为D(﹣1,4),与 轴交于点C(0,3),与
轴交于点C(0,3),与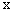 轴交于A,B两点(点A在点B的左侧)。
轴交于A,B两点(点A在点B的左侧)。
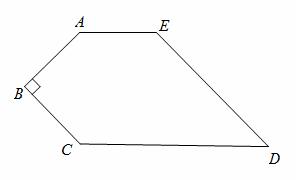


 A;
A; ,并求出使
,并求出使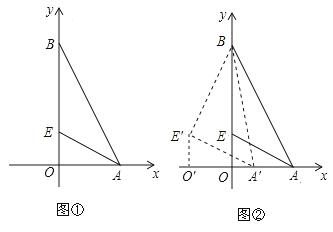
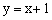 ,直接写出:①过原点且与l1垂直的直线l2的函数表达式;②过点(1,0)且与l1垂直的直线l2的函数表达式;
,直接写出:①过原点且与l1垂直的直线l2的函数表达式;②过点(1,0)且与l1垂直的直线l2的函数表达式; 向与x轴的正方
向与x轴的正方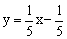 垂直的直线l6的函数表达式。
垂直的直线l6的函数表达式。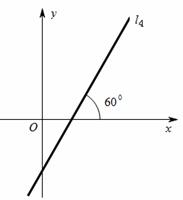
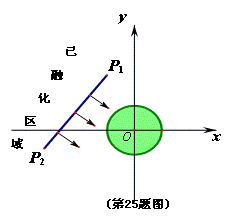
 营O为圆心,半径为4km 圆形考察区域,线段P1、P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整
营O为圆心,半径为4km 圆形考察区域,线段P1、P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整 数)的关系是
数)的关系是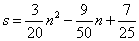
 .以O为原
.以O为原