题目内容
关于未知数x的方程ax2-
x-1=0有两个实数解,则a的取值范围是( )
| 5-a |
A、a≥-
| ||
| B、0<a≤5 | ||
C、-
| ||
| D、0<a≤5,且a≠0 |
考点:根的判别式,一元二次方程的定义
专题:
分析:由于关于x的方程ax2-
x-1=0有两个实数解,当a≠0时,方程为一元二次方程,那么它的判别式的值是一个非负数,由此即可求出a的取值范围.
| 5-a |
解答:解:当a≠0时,方程为一元二次方程,
∴△=b2-4ac=5-a+4a≥0,
即5-a+4a≥0且5-a≥0,
解得a≥-
,a≤5
所以根据两种情况得a的取值范围是-
≤a≤5.
故选:C.
∴△=b2-4ac=5-a+4a≥0,
即5-a+4a≥0且5-a≥0,
解得a≥-
| 5 |
| 3 |
所以根据两种情况得a的取值范围是-
| 5 |
| 3 |
故选:C.
点评:此题考查一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
此题切记不要忽略一元二次方程二次项系数不为零这一隐含条件.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
此题切记不要忽略一元二次方程二次项系数不为零这一隐含条件.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
直角三角形一边长为8,另一条边是方程x2-2x-24=0的一解,则此直角三角形的第三条边长是( )
| A、10 | ||
B、2
| ||
| C、4或10 | ||
D、10或2
|
下列计算正确的是( )
| A、3ab-2ab=1 | ||||
B、(
| ||||
| C、-(-a)4÷a2=a2 | ||||
D、(
|
 已知如图直线AB∥CD,∠A=40°且AE=AF,则∠DCF=( )
已知如图直线AB∥CD,∠A=40°且AE=AF,则∠DCF=( )| A、110° | B、120° |
| C、130° | D、140° |
已知∠α=30°,则∠α的余角是( )
| A、60° | B、70° |
| C、150° | D、30° |
 如图,AB、CD、EF相交于点O,∠1=20°,∠BOC=80°,则∠2=
如图,AB、CD、EF相交于点O,∠1=20°,∠BOC=80°,则∠2=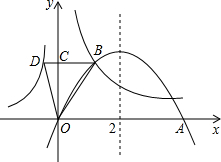 如图,对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,与反比例函数
如图,对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,与反比例函数