题目内容
6.设α、β是方程(x+1)(x-4)=-5的两实数根,则$\frac{{β}^{3}}{α}+\frac{{α}^{3}}{β}$=47.分析 根据α、β是方程(x+1)(x-4)=-5的两实数根,得到α+β=3,αβ=1,根据完全平方公式得到α4+β4=47,于是得到结论.
解答 解:方程(x+1)(x-4)=-5可化为x2-3x+1=0,
∵α、β是方程(x+1)(x-4)=-5的两实数根,
∴α+β=3,αβ=1,
∴α2+β2=(α+β)2-2αβ=7,α4+β4=(α2+β2)2-2α2•β2=47,
∴$\frac{{β}^{3}}{α}+\frac{{α}^{3}}{β}$=$\frac{{α}^{4}+{β}^{4}}{αβ}$=47,
故答案为:47.
点评 本题考查了根与系数的关系,难度较大,关键是根据已知条件对$\frac{{β}^{3}}{α}+\frac{{α}^{3}}{β}$进行变形.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
17.关于2、6、1、10、6的这组数据,下列说法正确的是( )
| A. | 这组数据的众数是6 | B. | 这组数据的中位数是1 | ||
| C. | 这组数据的平均数是6 | D. | 这组数据的方差是10 |
11.若x=-3,y=1,则代数式2x-3y+1的值为( )
| A. | -10 | B. | -8 | C. | 4 | D. | 10 |
15.某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
则他们捐款金额的中位数和平均数分别是( )
| 金额/元 | 5 | 10 | 20 | 50 | 100 |
| 人数 | 4 | 16 | 15 | 9 | 6 |
| A. | 10,20.6 | B. | 20,20.6 | C. | 10,30.6 | D. | 20,30.6 |
 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.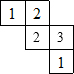 由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其中正方形中的数字表示该位置上的小正方体的个数,那么该几何体的主视图是( )
由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其中正方形中的数字表示该位置上的小正方体的个数,那么该几何体的主视图是( )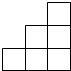

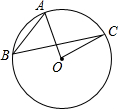 如图,OA、OC是⊙O的半径,点B在⊙O上,连接AB、BC,若∠ABC=40°,则∠AOC=80度.
如图,OA、OC是⊙O的半径,点B在⊙O上,连接AB、BC,若∠ABC=40°,则∠AOC=80度.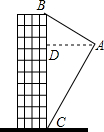 如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)
如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)