题目内容
6. 已知二次函数y=-x2+2x+m.
已知二次函数y=-x2+2x+m.(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
分析 (1)由二次函数的图象与x轴有两个交点,得到△=22+4m>0于是得到m>-1;
(2)把点A(3,0)代入二次函数的解析式得到m=3,于是确定二次函数的解析式为:y=-x2+2x+3,求得B(0,3),得到直线AB的解析式为:y=-x+3,把对称轴方程x=1,代入直线y=-x+3即可得到结果.
解答 解:(1)∵二次函数的图象与x轴有两个交点,
∴△=22+4m>0
∴m>-1;
(2)∵二次函数的图象过点A(3,0),
∴0=-9+6+m
∴m=3,
∴二次函数的解析式为:y=-x2+2x+3,
令x=0,则y=3,
∴B(0,3),
设直线AB的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{0=3k+b}\\{3=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线AB的解析式为:y=-x+3,
∵抛物线y=-x2+2x+3,的对称轴为:x=1,
∴把x=1代入y=-x+3得y=2,
∴P(1,2).
点评 本题考查了二次函数与x轴的交点问题,求函数的解析式,知道抛物线的对称轴与直线AB的交点即为点P的坐标是解题的关键.

练习册系列答案
相关题目
16.下列各组中,不是同类项的是( )
| A. | 52与25 | B. | -ab与ba | C. | 0.2a2b与-$\frac{1}{5}$a2b | D. | a2b3与-a3b2 |
17.若(x-1)2-9=0,则x=( )
| A. | ±9 | B. | ±3 | C. | 4或-2 | D. | -4或2 |
1.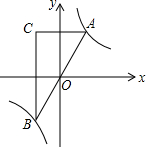 如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
 如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )| A. | n=-2m | B. | n=-$\frac{2}{m}$ | C. | n=-4m | D. | n=-$\frac{4}{m}$ |
15.五箱南丰贡桔的质量(单位:kg)分别为:8,10,11,8,9,则这五箱贡桔质量的中位数和众数分别为( )
| A. | 10和8 | B. | 10和9 | C. | 9和8 | D. | 8和8 |
16.下列各组数都是无理数的是( )
| A. | 0.2,$\sqrt{3}$ | B. | $\frac{\sqrt{2}}{3}$,$\sqrt{4}$ | C. | $\frac{4}{5}$,0 | D. | 2$\sqrt{3}$,$\sqrt{5}$+$\sqrt{3}$ |

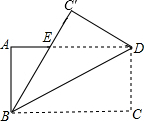 如图,将矩形ABCD沿对角线BD折叠,使点C与C′重合.若AB=3,则C′D的长为3.
如图,将矩形ABCD沿对角线BD折叠,使点C与C′重合.若AB=3,则C′D的长为3.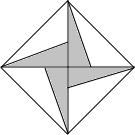 如图,正方形的阴影部分是由四个直角边长都是1和3的直角三角形组成的,假设可以在正方形内部随意取点,那么这个点取在阴影部分的概率为$\frac{1}{3}$.
如图,正方形的阴影部分是由四个直角边长都是1和3的直角三角形组成的,假设可以在正方形内部随意取点,那么这个点取在阴影部分的概率为$\frac{1}{3}$.