题目内容
8.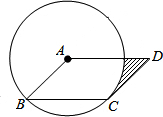 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,已知半径AB=2,则图中阴影部分面积为(2-$\frac{π}{2}$)cm2.
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,已知半径AB=2,则图中阴影部分面积为(2-$\frac{π}{2}$)cm2.
分析 连接AC,过点C作CE⊥AD于点E,根据切线的性质可知AC⊥CD,再由四边形ABCD是平行四边形可知AB=CD=AC,故△ACD是等腰直角三角形,根据勾股定理求出AD的长,由等腰三角形的性质得出AE的长,故可得出CE的长,再由S阴影=S平行四边形ABCD-S△ABC-S扇形CAF即可得出结论.
解答 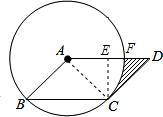 解:连接AC,过点C作CE⊥AD于点E,
解:连接AC,过点C作CE⊥AD于点E,
∵CD是⊙O的切线,
∴AC⊥CD.
∵四边形ABCD是平行四边形,
∴AB=CD=AC,
∴△ACD是等腰直角三角形.
∵AB=2,
∴AD=$\sqrt{{AC}^{2}+{CD}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴AE=$\frac{1}{2}$AD=$\sqrt{2}$,
∴CE=AE=$\sqrt{2}$.
∴S阴影=S平行四边形ABCD-S△ABC-S扇形CAF
=2$\sqrt{2}$×$\sqrt{2}$-$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{2}$-$\frac{45π×{2}^{2}}{360}$
=(2-$\frac{π}{2}$)cm2.
故答案为:(2-$\frac{π}{2}$)cm2.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
18.△ABC中,AB=AC,BC=8,则△ABC的周长x的取值范围是( )
| A. | x>4 | B. | 8<x<16 | C. | 16<x<24 | D. | x>16 |
16.通过平移y=-2(x-1)2+3的图象,可得到y=-2x2的图象,下列平移方法正确的是( )
| A. | 向左移动1个单位,向上移动3个单位 | |
| B. | 向右移动1个单位,向上移动3个单位 | |
| C. | 向左移动1个单位,向下移动3个单位 | |
| D. | 向右移动1个单位,向下移动3个单位 |
3. 如图,以直角三角形的三边作正方形,已知S1=9,S2=36,S3=4,正方形S的边长为8,则S4=( )
如图,以直角三角形的三边作正方形,已知S1=9,S2=36,S3=4,正方形S的边长为8,则S4=( )
 如图,以直角三角形的三边作正方形,已知S1=9,S2=36,S3=4,正方形S的边长为8,则S4=( )
如图,以直角三角形的三边作正方形,已知S1=9,S2=36,S3=4,正方形S的边长为8,则S4=( )| A. | 12 | B. | 14 | C. | 15 | D. | 16 |
17.下列关于多项式5xy2-6x2yz-1的说法中,正确的是( )
| A. | 它是三次三项式 | B. | 它是四次两项式 | ||
| C. | 它的最高次项是-6x2yz | D. | 它的常数项是1 |
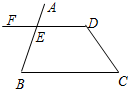 如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.
如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.