题目内容
8. 如图,已知菱形ABCD的周长20,sin∠ABD=$\frac{3}{5}$,求菱形ABCD的面积.
如图,已知菱形ABCD的周长20,sin∠ABD=$\frac{3}{5}$,求菱形ABCD的面积.
分析 根据菱形的性质结合勾股定理得出AC,BD的长,进而求出菱形面积.
解答  解:连接AC,
解:连接AC,
∵菱形ABCD的周长20,
∴AB=AD=BC=CD=5,
∵菱形对角线平分且互相垂直,
∴AC⊥BD,
∵sin∠ABD=$\frac{3}{5}$,
∴$\frac{AO}{AB}$=$\frac{3}{5}$,
则AO=3,BO=4,
故AC=6,BD=8,
则菱形ABCD的面积为:$\frac{1}{2}$×6×8=24.
点评 此题主要考查了菱形的性质以及勾股定理等知识,正确得出菱形对角线的长是解题关键.

练习册系列答案
相关题目
13. 已知一次函数y=kx+b的图象如图所示,则关于x的不等式k(x-4)-2b≥0的解集为( )
已知一次函数y=kx+b的图象如图所示,则关于x的不等式k(x-4)-2b≥0的解集为( )
 已知一次函数y=kx+b的图象如图所示,则关于x的不等式k(x-4)-2b≥0的解集为( )
已知一次函数y=kx+b的图象如图所示,则关于x的不等式k(x-4)-2b≥0的解集为( )| A. | x≥-2 | B. | x≤-2 | C. | x≤3 | D. | x≥3 |
 如图,两同心圆⊙O,其半径分别为5和3,大圆的弦AB与小圆相切于点C,则AB的长为8.
如图,两同心圆⊙O,其半径分别为5和3,大圆的弦AB与小圆相切于点C,则AB的长为8.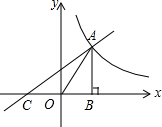 如图,已知一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为4,则AC的长为4$\sqrt{2}$(保留根号).
如图,已知一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为4,则AC的长为4$\sqrt{2}$(保留根号).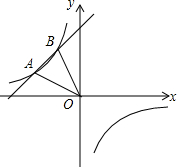 如图,一次函数的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-4,a)、B两点,点B的横坐标比点A的横坐标大2,且S△AOB=6.
如图,一次函数的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-4,a)、B两点,点B的横坐标比点A的横坐标大2,且S△AOB=6.