题目内容
18. 如图,两同心圆⊙O,其半径分别为5和3,大圆的弦AB与小圆相切于点C,则AB的长为8.
如图,两同心圆⊙O,其半径分别为5和3,大圆的弦AB与小圆相切于点C,则AB的长为8.
分析 如图连接AO、OC,根据切线的性质以及垂径定理,在RT△AOC中利用勾股定理即可解决.
解答 解:如图连接AO、OC.
∵AB是⊙O切线,
∴OC⊥AB,AC=BC,
在RT△AOC中,∵∠ACO=90°,OA=5,OC=3,
∴AC=$\sqrt{A{O}^{2}-O{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AB=2AC=8.
故答案为8
点评 本题考查切线的性质、垂径定理.勾股定理等知识,解题的关键是熟练运用这些知识解决问题,属于基础题中考常考题型.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
6.下列命题错误的是( )
| A. | 平行四边形的对角线互相平分 | |
| B. | 对角线互相垂直平分的四边形是菱形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线相等的四边形是正方形 |
10.一个角的余角是30°,则这个角的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 70° |
7. 如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )
如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )
 如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )
如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,∠1=35°,则∠2的度数是( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
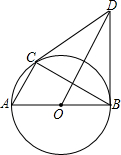 如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD.
如图,⊙O是Rt△ABC的外接圆,点O在AB上,BD⊥AB,点B是垂足,OD∥AC,连接CD. 如图,在矩形ABCD中,AB=2,BC=4,M是AD的中点,动点E在线段AB上,连结EM并延长交射线CD于点F,过点M作EF的垂线交BC于点G,连结EG、FG.
如图,在矩形ABCD中,AB=2,BC=4,M是AD的中点,动点E在线段AB上,连结EM并延长交射线CD于点F,过点M作EF的垂线交BC于点G,连结EG、FG. 如图,已知菱形ABCD的周长20,sin∠ABD=$\frac{3}{5}$,求菱形ABCD的面积.
如图,已知菱形ABCD的周长20,sin∠ABD=$\frac{3}{5}$,求菱形ABCD的面积.