题目内容
20．
如图，在Rt△ABC中，∠BAC=90°，AD⊥BC，∠B=30°，CD=1，求AD，BD．
分析 根据含30°角的直角三角形的性质即可得到结论．
解答 解：∵∠BAC=90°，AD⊥BC，
∴∠C+∠B=∠C+∠CAD=90°，
∵∠B=30°，
∴∠ACD=30°，
∵CD=1，
∴AC=2，AD=$\sqrt{3}$CD=$\sqrt{3}$，
∴BC=2AC=4，
∴BD=3．
点评 本题考查了含30°角的直角三角形的性质，熟记此限制是解题的关键．
练习册系列答案
相关题目
10．已知xa+a=3是关于x的一元一次方程，则该方程的解为（ ）
| A． | x=1 | B． | x=2 | C． | x=3 | D． | x=4 |
8．
如图，为估计池塘岸边A、B两点间的距离，在池塘的一侧选取点O，分别取OA、OB的中点M、N，测得MN=40m，则A、B两点间的距离是（ ）
如图，为估计池塘岸边A、B两点间的距离，在池塘的一侧选取点O，分别取OA、OB的中点M、N，测得MN=40m，则A、B两点间的距离是（ ）| A． | 20m | B． | 80m | C． | 120m | D． | 160m |
15．甲、乙两名队员参加射击训练，成绩分布被制成下列两个统计图：
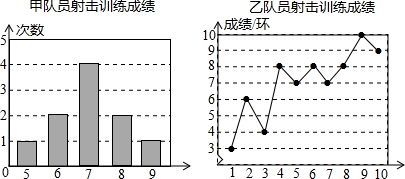
根据以上信息，整理分析数据如下：
（1）写出表格中a，b，c的值；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？
根据以上信息，整理分析数据如下：
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | 7 | b | 7 | c |
| 乙 | a | 7.5 | 8 | 4.2 |
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？
5．
如图，以∠AOB的顶点为圆心，取适当长为半径画弧，交OA于点C，交OB于点D，再分别以点C、D为圆心，大于$\frac{1}{2}$CD的长为半径画弧，两弧在∠AOB内部交于点E，过点E作射线OE，连接CD．则下列说法错误的是（ ）
如图，以∠AOB的顶点为圆心，取适当长为半径画弧，交OA于点C，交OB于点D，再分别以点C、D为圆心，大于$\frac{1}{2}$CD的长为半径画弧，两弧在∠AOB内部交于点E，过点E作射线OE，连接CD．则下列说法错误的是（ ）| A． | 射线OE是∠AOB的平分线 | B． | O、E两点关于CD所在直线对称 | ||
| C． | △COD是等腰三角形 | D． | C、D两点关于OE所在直线对称 |
9．
在△ABC中，已知∠C=90°，BC=3，AC=4，则它的内切圆⊙O的半径是（ ）
在△ABC中，已知∠C=90°，BC=3，AC=4，则它的内切圆⊙O的半径是（ ）| A． | 1 | B． | 2 | C． | 2.5 | D． | 5 |