题目内容
1.化简|x+1|+|x+2|.分析 先分别令x+1=0、x+2=0分别求出x的对应值,再根据x的取值范围利用绝对值的性质去掉绝对值符号即可.
解答 解:∵x+1=0、x+2=0分别求得:x=-1,x=-2,
∴当x<-2时,原式=-(x+1)-(x+2)=-2x-3;
当-2≤x<-1时,原式=-(x+1)+(x+2)=1;
当x≥-1时,原式=(x+1)+(x+2)=2x+3.
点评 本题考查的是绝对值的性质,整式的加减,在解答此题时要注意应用分类讨论的思想,不要漏解.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
10.若$\frac{a}{b}>0$,$\frac{c}{b}<0$,则ac( )
| A. | 大于0 | B. | 小于0 | C. | 不一定 | D. | 等于0 |
11.下列说法中正确的是( )
| A. | 比正数小的数一定都是负数 | |
| B. | 几个负数相加,和一定是负数 | |
| C. | 减去一个负数,等于加上一个非负数 | |
| D. | 两个负数相减,差一定是负数 |
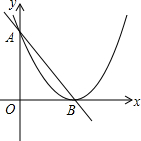 如图,直线y=-x+3交x轴于点B,交y轴于点A.抛物线的顶点为点B,且经过点A.
如图,直线y=-x+3交x轴于点B,交y轴于点A.抛物线的顶点为点B,且经过点A.