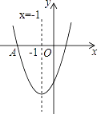题目内容
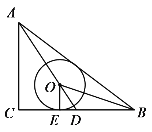
【题目】如图，
的直径为
，点
在圆周上（异于
，
），
．
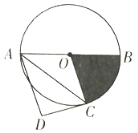
（1）若
，
，求图中扇形
的面积．
（2）若
是
的平分线，求证：直线
是的切线．
【答案】（1）
；（2）证明见解析．
【解析】
（1）根据圆周角定理确定圆心角
，然后运用扇形的面积公式即可；
（2）先根据角平分线的性质和相似三角形的知识得到∠OCA=∠CAD，OC//AD；再根据AD⊥CD ，得到OC⊥CD即可证明结论．
解：（1）
，
，
，
；
（2）证明：∵AC是∠DAB的角平分线
∴∠OAC=∠DAC
∵OA=OC
∴∠0AC=∠OCA
∴∠DAC=∠OCA
∴OC//AD
又∵AD⊥DC.
∴OC⊥CD
∴DC是00的切线．
本题主要考查的是圆周角定理、求扇形的面积、切线的判定方法，掌握切线的判定方法是解答本题的关键．
【题目】随着国内疫情基本得到控制，旅游业也慢慢复苏，经市场调研发现旅游景点未来
天内，旅游人数
与时间
的关系如下表；每张门票
与时间之间存在如下图所示的一次函数关系．（
，且为整数）
时间 |
|
|
|
|
|
人数 |
|
|
|
|
|
<>
请结合上述信息解决下列问题：
（1）直接写出：关于的函数关系式是 ．与时间函数关系式是 ．
（2）请预测未来天中哪一天的门票收入最多，最多是多少？
（3）为支援武汉抗疫，该旅游景点决定从每天获得的门票收入中拿出
元捐赠给武汉红十字会，求捐款后共有几天每天剩余门票收入不低于
元？
【题目】参照学习函数的过程方法，探究函数
的图像与性质，因为
，即
，所以我们对比函数
来探究列表：
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 | <> |
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点：在平面直角坐标系中以自变量
的取值为横坐标，以
相应的函数值为纵坐标，描出相应的点如图所示：
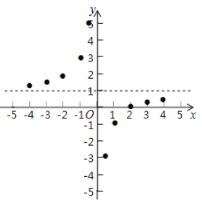
（1）请把
轴左边各点和右边各点分别用一条光滑曲线，顺次连接起来；
（2）观察图象并分析表格，回答下列问题：
①当
时，随的增大而______；（“增大”或“减小”）
②的图象是由的图象向______平移______个单位而得到的；
③图象关于点______中心对称.（填点的坐标）
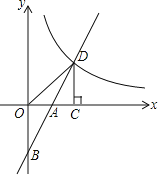
（3）函数与直线
交于点
，
，求
的面积.
