Question

Rt△OAB的顶点与坐标原点重合∠AOB=90°，AO=3BO，已知当点A在反比例函数y=

9

x

（x＞0）图象上移动时，点B也在某一反比例函数图象上，求该函数的解析式．

Answer 1

考点：待定系数法求反比例函数解析式

专题：

分析：首先设B点坐标满足的函数解析式是y=

k

x

，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，易得△AOC∽△OBD，然后由相似三角形面积比等于相似比的平方，求得S_△AOC：S_△BOD=9，继而求得答案．

解答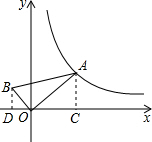：解：设B点坐标满足的函数解析式是y=

k

x

，
过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，
∴∠ACO=∠BDO=90°，
∴∠AOC+∠OAC=90°，
∵∠AOB=90°，
∴∠AOC+∠BOD=90°，
∴∠BOD=∠OAC，
∴△AOC∽△OBD，
∴S_△AOC：S_△BOD=（

OA

OB

）²，
∵AO=3BO，
∴S_△AOC：S_△BOD=9，
∵S_△AOC=

1

2

OC•AC=

1

2

×9=

9

2

，S_△BOD=

1

2

OD•BD=

1

2

|k|，
∴k=-1，
∴B点坐标满足的函数解析式是y=-

1

x

．

点评：此题考查了待定系数法求反比例函数的解析式，相似三角形的判定与性质以及反比例函数的性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．