题目内容
10. 如图,已知点O在线段AB上,点C、D分别是AO、BO的中点
如图,已知点O在线段AB上,点C、D分别是AO、BO的中点(1)AO=2CO;BO=2DO;
(2)若CO=3cm,DO=2cm,求线段AB的长度;
(3)若线段AB=10,小明很轻松地求得CD=5.他在反思过程中突发奇想:若点O在线段AB的延长线上,原有的结论“CD=5”是否仍然成立呢?请帮小明画出图形分析,并说明理由.
分析 (1)根据线段中点的性质,可得答案;
(2)根据线段中点的性质,可得AO,BO的长,根据线段的和差,可得答案;
(3)O是AB延长线上的一点,由C、D分别是线段AO,BO的中点可得出CO,DO分别是AO,BO的一半,因此,CO,DO的差的一半就等于AO,BO差的一半,因为,CD=CO-DO,AB=AO-BO,根据上面的分析可得出CD=$\frac{1}{2}$AB.因此结论是成立的.
解答 解:(1)∵点C、D分别是AO、BO的中点
∴AO=2CO;BO=2DO;
故答案为:2;2.
(2))∵点C、D分别是AO、BO的中点,CO=3cm,DO=2cm,
∴AO=2CO=6cm;BO=2DO=4cm,
∴AB=AO+BO=6+4=10cm.
(3)仍然成立,
如图: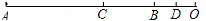
理由:∵点C、D分别是AO、BO的中点,
∴CO=$\frac{1}{2}$AO;DO=$\frac{1}{2}$BO,
∴CD=CO-DO=$\frac{1}{2}$AO-$\frac{1}{2}$BO=$\frac{1}{2}$(AO-BO)=$\frac{1}{2}AB$=$\frac{1}{2}×10$=5cm.
点评 本题考查了两点间的距离,解决本题的关键是利用了线段中点的性质,线段的和差得出答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 如图,数轴上的点A表示的有理数可能是( )
如图,数轴上的点A表示的有理数可能是( )
 如图,数轴上的点A表示的有理数可能是( )
如图,数轴上的点A表示的有理数可能是( )| A. | -3 | B. | -2 | C. | -2.5 | D. | -3.5 |
20.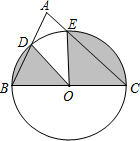 如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )
如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )
 如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )
如图,△ABC中,∠A=70°,BC=2,以BC为直径的⊙O与AB、BC边交于D、E两点,则图中阴影的面积为( )| A. | $\frac{7}{18}π$ | B. | $\frac{7}{9}π$ | C. | $\frac{14}{9}π$ | D. | $\frac{28}{9}π$ |
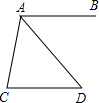 如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D等于多少度?
如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D等于多少度?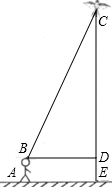 身高1.6米的小明想利用“勾股定理”测得下图风筝CE的高度,于是他测得BD的长度为25米,并根据手中剩余线的长度计算出风筝线BC的长为65米.求风筝的高度CE.
身高1.6米的小明想利用“勾股定理”测得下图风筝CE的高度,于是他测得BD的长度为25米,并根据手中剩余线的长度计算出风筝线BC的长为65米.求风筝的高度CE.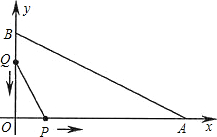 如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?