题目内容
5.己知反比例函数y=$\frac{6}{x}$,当1<x<3时,y的取值范围是( )| A. | 0<y<l | B. | 1<y<2 | C. | 2<y<6 | D. | y>6 |
分析 利用反比例函数的性质,由x的取值范围并结合反比例函数的图象解答即可.
解答 解:∵k=6>0,
∴在每个象限内y随x的增大而减小,
又∵当x=1时,y=6,
当x=3时,y=2,
∴当1<x<3时,2<y<6.
故选C.
点评 本题主要考查反比例函数的性质,当k>0时,在每一个象限内,y随x的增大而减小;当k<0时,在每一个象限,y随x的增大而增大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.cos45°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
17.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
则通话时间不超过15min的频率为( )
| 通话时间x/min | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
| 频数(通话次数) | 20 | 16 | 9 | 5 |
| A. | 0.1 | B. | 0.4 | C. | 0.5 | D. | 0.9 |
15.不等式组$\left\{\begin{array}{l}x+1>0\\ x-1≤1\end{array}\right.$的解集是( )
| A. | x≤2 | B. | x>-1 | C. | -1<x≤2 | D. | 无解 |
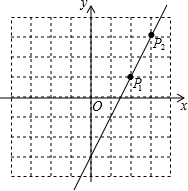 如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.
如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.

 如图,在△ABC中,DE∥BC,分别交AB,AC于点D、E.若AD=3,DB=2,BC=6,则DE的长为3.6.
如图,在△ABC中,DE∥BC,分别交AB,AC于点D、E.若AD=3,DB=2,BC=6,则DE的长为3.6. 如图,已知二次函数y=x2+(1-m)x-m(其中0<m<1)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC
如图,已知二次函数y=x2+(1-m)x-m(其中0<m<1)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC