题目内容
14.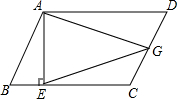 已知:在?ABCD中,AE⊥BC,垂足为E,点G为CD上的中点,
已知:在?ABCD中,AE⊥BC,垂足为E,点G为CD上的中点,(1)若CG=2,AE=3,求BE的长;
(2)求证:∠CEG=$\frac{1}{2}$∠AGE.
分析 (1)首先求出DC=AB=4,根据勾股定理求出BE即可;
(2)过G作GM⊥AE于M,利用平行线分线段成比例定理,求出M为AE中点,得出等腰三角形AGE,根据性质得出GM是∠AGE的角平分线,即可得出答案.
解答 (1)解:∵四边形ABCD是平行四边形,
∴AB=CD,
∵点G为CD的中点,CG=2,
∴DC=AB=4,
∵AE⊥BC,
∴∠AEB=90°,
在Rt△ABE中,由勾股定理得:BE=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$;
(2)证明:过G作GM⊥AE于M,
∵AE⊥BE,GM⊥AE,
∴GM∥BC∥AD,
∴CG=DG,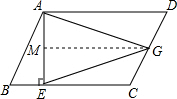
∴AM=ME(一组平行线在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等),
∵GM⊥AE,
∴AG=EG,
∴∠AGM=∠EGM,
∴∠AGE=2∠MGE,
∵GM∥BC,
∴∠EGM=∠CEG,
∴∠CEG=$\frac{1}{2}$∠AGE.
点评 本题考查了平行四边形性质、等腰三角形的性质和判定、平行线分线段成比例定理、勾股定理等知识点的应用,得出AG=EG是解题关键.

练习册系列答案
相关题目
7.一元二次方程x2+2=0的根的情况为( )
| A. | 没有实根 | B. | 有两个相等的实根 | ||
| C. | 有两个不等的实根 | D. | 有两个实根 |
6.下列运算中,正确的是( )
| A. | b3•b3=b9 | B. | (-x3y)•(xy2)=x4y3 | C. | (-2x3)2=-4x6 | D. | (-a2)3=-a6 |
4.森林是地球之肺,每年平均能为人类提供大约28.3亿吨的有机物,十年所提供的有机物用科学记数法表示为( )
| A. | 2.83×107吨 | B. | 2.83×108吨 | C. | 2.83×109吨 | D. | 2.83×1010吨 |
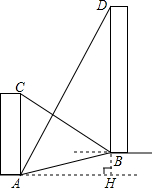 如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2$\sqrt{3}$,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2$\sqrt{3}$,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
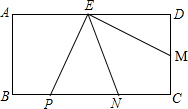 已知矩形ABCD中,AD=2AB,AB=6,E为AD中点,M为CD上一点,PE⊥EM交CB于点P,EN平分∠PEM交BC于点N.
已知矩形ABCD中,AD=2AB,AB=6,E为AD中点,M为CD上一点,PE⊥EM交CB于点P,EN平分∠PEM交BC于点N.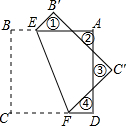 如图,正方形纸片ABCD的边长为4,将其沿EF折叠,则图中①②③④四个三角形的周长之和为16.
如图,正方形纸片ABCD的边长为4,将其沿EF折叠,则图中①②③④四个三角形的周长之和为16.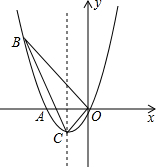 已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C
已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C