题目内容
17.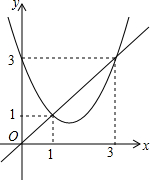 二次函数y=x2+bx+c与直线y=x的图象如图所示,有以下结论:
二次函数y=x2+bx+c与直线y=x的图象如图所示,有以下结论:①b2-4c>0;②3b+c+6=0;③当x2+bx+c>1时,x<1;④当x2+bx+c>$\frac{9}{8x}$时,x>$\frac{3}{2}$;⑤当1<x<3时,x2+(b-1)x+c<0.
其中正确结论的编号是②⑤.
分析 ①根据图象与x轴的交点情况判断b2-4c的符号;
②根据图象经过(3,3),判断3b+c+6=0的正确性;
③根据图象可以判断③;
④根据过顶点($\frac{3}{2}$,$\frac{3}{4}$)的反比例函数为y=$\frac{9}{8x}$,判断④;
⑤根据当1<x<3时,二次函数值小于一次函数值,列式判断⑤.
解答 解:∵函数y=x2+bx+c与x轴无交点,
∴b2-4ac<0;
∴b2-4c<0
故①不正确;
当x=3时,y=9+3b+c=3,
∴3b+c+6=0
故②正确;
从图象可知当x2+bx+c>1时,x<1或x>2
③不正确;
④过顶点($\frac{3}{2}$,$\frac{3}{4}$)的反比例函数为y=$\frac{9}{8x}$,
由图象可知,当x2+bx+c>$\frac{9}{8x}$时,x>$\frac{3}{2}$或x<0,
④错误.
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b-1)x+c<0.
故⑤正确.
故答案为:②⑤
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
5.下列运算不正确的是( )
| A. | x2•x3=x5 | B. | (x2)3=x6 | C. | (-2x)3=-8x3 | D. | x3+x3=2x6 |
2.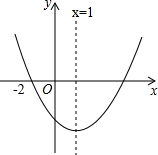 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0,
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0,
②2a-b=0,③当-2<x<3时,y<0,④当x≥1时,y随x的增大而减小,正确
的个数是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0,
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0,②2a-b=0,③当-2<x<3时,y<0,④当x≥1时,y随x的增大而减小,正确
的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )| A. | a>0 | B. | b>0 | C. | c<0 | D. | a+b+c<0 |
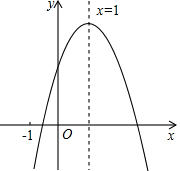 二次函数y=ax2+bx+c的图象如图所示,有下列4个结论:
二次函数y=ax2+bx+c的图象如图所示,有下列4个结论: