题目内容
16.如图,在正方形ABCD中,动点P在射线CB上(与B、C不重合),连结AP,过D作DF∥AP交直线BC于点F,过F作FE⊥直线BD于点E,连结AE、PE.(1)如图1,当点P在线段CB上时
①求证:△ABP≌△DCF;
②点P在运动过程中,探究:△AEP的形状是否发生变化,若不变,请判断△AEP的形状,并说明理由;
(2)如图2,当点P在CB的延长线上时
①(1)中的结论②是否成立?不必说明理由;
②若正方形ABCD的边长为1,设BP=x,当x为何值时,DF平分∠BDC?
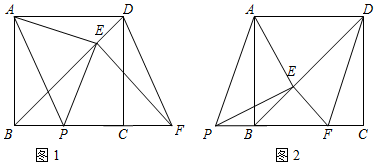
分析 (1)①根据正方形的性质得到AB=DC,∠ABC=∠DCF=90°,利用AAS定理证明△ABP≌△DCF;
②证明△ABE≌△CBE,得到AE=CE,∠AEB=∠CEB,证明△EBP≌△EFC,根据全等三角形的性质证明;
(2)①利用与(1)相似的方法解答;
②根据角平分线的性质列出方程,解方程即可.
解答 (1)①证明:∵四边形ABCD是正方形,
∴AB=DC,∠ABC=∠DCF=90°,
∵DF∥AP,
∴∠APB=∠DFC,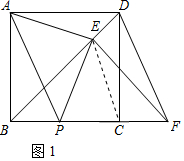
在△ABP和△DCF中,
$\left\{\begin{array}{l}{∠APB=∠DFC}\\{∠ABP=∠DCF}\\{AB=DC}\end{array}\right.$,
∴△ABP≌△DCF;
②△AEP的形状不发生变化,△AEP是等腰直角三角形,
理由:连结CE,
在△ABE和△CBE中,
$\left\{\begin{array}{l}{BA=BC}\\{∠ABE=∠CBE}\\{BE=BE}\end{array}\right.$,
∴△ABE≌△CBE,
∴AE=CE,∠AEB=∠CEB,
∵FE⊥BD,∠EBF=45°,
∴EB=EF,∠EBF=∠EFB=45°
∵△ABP≌△DCF,
∴BP=FC,
∴△EBP≌△EFC,
∴EP=EC,∠BEP=∠FEC,
∴AE=EP,
∠AEB+∠BEP=∠BEC+∠CEF=90°,
∴△AEP是等腰直角三角形;
(2)①(1)中的结论②成立,
证明方法与(1)相同;
②若DF平分∠BDC,
则EF=CF,
∵CF=BP=x,
∴BF=1-x,
∵△BEF是等腰直角三角形
∴BF=$\sqrt{2}$EF,
∴1-x=$\sqrt{2}$x,
解得x=$\sqrt{2}$-1,
∴当x=$\sqrt{2}$-1时,DF平分∠BDC.
点评 本题考查的是正方形的性质、全等三角形的判定和性质、等腰直角三角形的性质,掌握相关的判定定理和性质定理是解题的关键.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{9}$ | D. | 1 |
| 等级 | 一分钟跳 绳次数x | 人数 |
| A | x>180 | 12 |
| B | 150<x≤180 | 14 |
| C | 120<x≤150 | a |
| D | x≤120 | b |
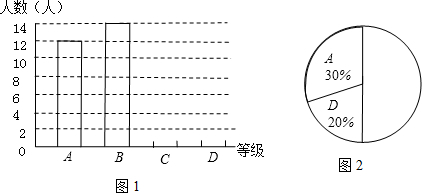
请结合图表完成下列问题:
(1)表1中a=6,b=8;
(2)请把图1和图2补充完整;
(3)已知该校有1000名九年级学生,若在一分钟内跳绳次数不大于120次的为不合格,则该校九年级学生一分钟跳绳不合格的学生估计为200人.
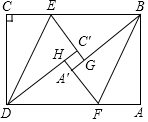 将一张矩形ABCD纸片,按如图进行折叠,分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE′与△A′BF,且边EC′的延长线与A′B交于点G,边FA的延长线与C′D交于一点H,已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=4,则线段BC=52.
将一张矩形ABCD纸片,按如图进行折叠,分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE′与△A′BF,且边EC′的延长线与A′B交于点G,边FA的延长线与C′D交于一点H,已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=4,则线段BC=52. 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上的一点,点E在BC边上,连接AE、DE、DC,AE=CD.求证:∠BAE=∠BCD.
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上的一点,点E在BC边上,连接AE、DE、DC,AE=CD.求证:∠BAE=∠BCD.
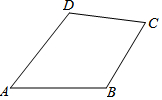 如图,在四边形ABCD中,AB=AD,CB=CD.请你添加一条线把它分成两个全等三角形,并给出证明.
如图,在四边形ABCD中,AB=AD,CB=CD.请你添加一条线把它分成两个全等三角形,并给出证明.