题目内容
晓丽的家住在D处,每天她要送女儿到正东方向,距离家2500米外的幼儿园B处,然后沿原路返回到离家正西1500米C处上班,晓丽的工作单位的正北方向上有一家超市A.恰好晓丽家所在点D在公路AB、AC夹角的平分线上,你能求出晓丽的工作单位距离超市A有多远吗?
考点:勾股定理的应用,全等三角形的应用,角平分线的性质
专题:
分析:根据角平分线的性质得出CD=DE,进而利用勾股定理得出BE的长,进而求出AB即可.
解答: 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,
∵AD平分∠CAB,DC⊥AC,DE⊥AB,
∴CD=DE,
∴BE2=
=2000(m),
设AC=x,则AE=x,
在Rt△ACB中,
AC2+BC2=AB2,
∴x2+40002=(x+2000)2,
解得x=3000.
答:晓丽的工作单位距离超市A为3000m.
 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,∵AD平分∠CAB,DC⊥AC,DE⊥AB,
∴CD=DE,
∴BE2=
| BD2-DE2 |
设AC=x,则AE=x,
在Rt△ACB中,
AC2+BC2=AB2,
∴x2+40002=(x+2000)2,
解得x=3000.
答:晓丽的工作单位距离超市A为3000m.
点评:此题主要考查了勾股定理的应用,直接利用勾股定理得出是解题关键.

练习册系列答案
相关题目
下列计算正确的是( )
| A、(a7)2=a9 |
| B、x3•x3=x9 |
| C、x6÷x3=x3 |
| D、2y2-6y2=-4 |
 如图,一轮船沿正东方向匀速航行,在A地测得小岛P在北偏东30°方向,此船航行1h到达B地时,测得小岛P在北偏东15°方向.
如图,一轮船沿正东方向匀速航行,在A地测得小岛P在北偏东30°方向,此船航行1h到达B地时,测得小岛P在北偏东15°方向. 某衬衫厂,生产某品牌衬衫的成本价位50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍,批发价不低于55元.
某衬衫厂,生产某品牌衬衫的成本价位50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍,批发价不低于55元. 如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA长为6,将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.
如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA长为6,将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.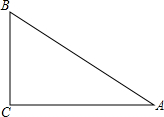 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.