题目内容
5.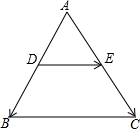 如图,已知在△ABC中,D、E分别是边AB、边AC的中点,$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AC}$=$\overrightarrow{n}$,那么向量$\overrightarrow{DE}$用向量$\overrightarrow{m}$,$\overrightarrow{n}$表示为$\frac{1}{2}$$\overrightarrow{n}$-$\frac{1}{2}$$\overrightarrow{m}$.
如图,已知在△ABC中,D、E分别是边AB、边AC的中点,$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AC}$=$\overrightarrow{n}$,那么向量$\overrightarrow{DE}$用向量$\overrightarrow{m}$,$\overrightarrow{n}$表示为$\frac{1}{2}$$\overrightarrow{n}$-$\frac{1}{2}$$\overrightarrow{m}$.
分析 由$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AC}$=$\overrightarrow{n}$,利用三角形法则求解即可求得$\overrightarrow{BC}$,又由在△ABC中,D、E分别是边AB、边AC的中点,可得DE是△ABC的中位线,然后利用三角形中位线的性质求解即可求得答案.
解答 解:∵$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AC}$=$\overrightarrow{n}$,
∴$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$=$\overrightarrow{n}$-$\overrightarrow{m}$,
∵在△ABC中,D、E分别是边AB、边AC的中点,
∴$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{1}{2}$($\overrightarrow{n}$-$\overrightarrow{m}$)=$\frac{1}{2}$$\overrightarrow{n}$-$\frac{1}{2}$$\overrightarrow{m}$.
故答案为:$\frac{1}{2}$$\overrightarrow{n}$-$\frac{1}{2}$$\overrightarrow{m}$.
点评 此题考查了平面向量的知识以及三角形中位线的性质.注意掌握三角形法则的应用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
13.当a>0时,下列关于幂的运算正确的是( )
| A. | a0=1 | B. | a-1=-a | C. | (-a)2=-a2 | D. | a${\;}^{\frac{1}{2}}$=$\frac{1}{{a}^{2}}$ |
10.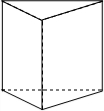 如图所示的三视图是主视图是( )
如图所示的三视图是主视图是( )
 如图所示的三视图是主视图是( )
如图所示的三视图是主视图是( )| A. |  | B. |  | C. |  | D. |  |
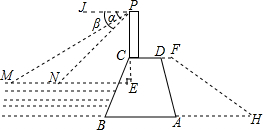 某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.瞭望台PC正前方水面上有两艘渔船M,N,观察员在瞭望台顶端P处观测渔船M的俯角α=31°,观测渔船N的俯角β=45°.已知MN所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.瞭望台PC正前方水面上有两艘渔船M,N,观察员在瞭望台顶端P处观测渔船M的俯角α=31°,观测渔船N的俯角β=45°.已知MN所在直线与PC所在直线垂直,垂足为点E,PE长为30米.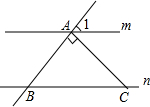 如图,直线m∥n,△ABC为等腰三角形,∠BAC=90°,则∠1=45度.
如图,直线m∥n,△ABC为等腰三角形,∠BAC=90°,则∠1=45度.