题目内容
一个两位数,十位上的数字比个位上的数字的4倍多1,将这两个数字调换顺序后所得数比原数小63,求原数.
考点:一元一次方程的应用
专题:
分析:设原两位数的个位数字为x,则十位数字为(4x+1),原来的两位数是:10(4x+1)+x,把十位上的数字与个位上的数字交换后,十位上数字是x,个位上数字是(4x+1),交换位置后这个数是:10x+(4x+1),列方程解答即可.
解答:解:设原两位数的个位数字为x,则十位数字为(4x+1),
依题意有:10x+(4x+1)+63=10(4x+1)+x,
解得:x=92.
所以原数为:92.
依题意有:10x+(4x+1)+63=10(4x+1)+x,
解得:x=92.
所以原数为:92.
点评:本题考查了一元一次方程的应用.根据数位知识及所给条件列出等量关系式解决问题的方法在数字问题中经常用到.

练习册系列答案
相关题目
 观察二次函数y=ax2+bx+c的图象.你认为其中错误的是( )
观察二次函数y=ax2+bx+c的图象.你认为其中错误的是( )| A、a<0 |
| B、c=0 |
| C、函数的最小值为-3 |
| D、当x<0时,y>0 |
 如图,⊙O中,半径OC⊥弦AB,∠BAC=20°,则∠AOC的度数是( )
如图,⊙O中,半径OC⊥弦AB,∠BAC=20°,则∠AOC的度数是( )| A、30° | B、40° |
| C、50° | D、60° |
 如图,已知?ABCD中,E是AB边上一点,且AE:EB=1:2,F是AD中点,则EO:OC=
如图,已知?ABCD中,E是AB边上一点,且AE:EB=1:2,F是AD中点,则EO:OC= 如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=3,则△ADE的周长是
如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=3,则△ADE的周长是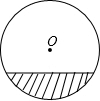 如图是一条水平铺设的直径为2米的通水管道横截面,当管道中水深为0.4米时,水面宽为
如图是一条水平铺设的直径为2米的通水管道横截面,当管道中水深为0.4米时,水面宽为