题目内容
7.先化简$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$-$\frac{x}{x-1}$,再从-1,1,2中选一个合适的数代入求值.分析 先化简原式,然后根据分式有意义的条件即可求出答案.
解答 解:原式=$\frac{(x+1)^{2}}{(x+1)(x-1)}$$-\frac{x}{x-1}$
=$\frac{x+1}{x-1}$-$\frac{x}{x-1}$
=$\frac{1}{x-1}$
∵$\left\{\begin{array}{l}{{x}^{2}-1≠0}\\{x-1≠0}\end{array}\right.$
∴x≠±1
当x=2时,
原式=$\frac{1}{2-1}$=1
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.?ABCD中,如果∠B=60°,则∠D的度数是( )
| A. | 20° | B. | 30° | C. | 60° | D. | 120° |
18.从A地到B地有一段上坡路和一段平路,如果车辆保持上坡每小时行驶30km,平路每小时行驶50km,下坡每小时行驶60km,那么车辆从A地到B地需要36分钟,从B地到A地需要21分钟,问A、B两地之间的坡路和平路各有多少千米?若设A、B两地之间的坡路为x km,平路为y km,根据题意可列方程组( )
| A. | $\left\{\begin{array}{l}{\frac{x}{30}+\frac{y}{50}=21}\\{\frac{x}{60}+\frac{y}{50}=36}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{30}+\frac{y}{50}=36}\\{\frac{x}{60}+\frac{y}{50}=21}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{30}+\frac{y}{50}=0.6}\\{\frac{x}{60}+\frac{y}{50}=0.35}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{30}+\frac{y}{50}=0.35}\\{\frac{x}{60}+\frac{y}{50}=0.6}\end{array}\right.$ |
12.已知下列四个命题:①对角线互相垂直平分的四边形是正方形;②对角线互相垂直且相等的四边形是菱形;③对角线互相平分且相等的四边形是矩形;④对角线互相平分、相等且垂直的四边形是正方形,其中真命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.不等式x-2≤0的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,AC∥DF,AB∥EF,若∠2=50°,则∠1=50°.
如图,AC∥DF,AB∥EF,若∠2=50°,则∠1=50°.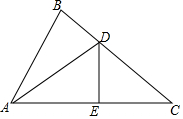 如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于E.
如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于E.