题目内容
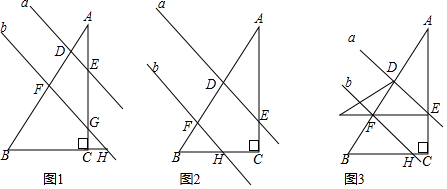
20.如图,△ABC是直角三角形,∠ACB=90°,两条平行直线a和b截△ABC如图所示,交点分别是D、E、F、G,直线b交直线BC于点H.(1)如图1,请证明∠AED+∠BHF=90°
(2)如图2,∠AED和∠BHF的数量关系是∠AED+∠BHF=90°
(3)如图3,在(2)的条件下,沿直线a将△ADE翻折,A与A′对立,若直线A′E∥BC,求证:2∠B-∠A′DB=90°.
分析 (1)先由平行线的性质得出∠AED=∠AGF,进而得出∠AED=∠CGH,再利用直角三角形的性质即可得出结论;
(2)先根据直角三角形的性质得出∠CGE+∠CEG=90°,再用平行线的性质和对顶角性质即可得出结论;
(3)先由平行线的性质得出∠AFE=∠B,再用三角形的外角得出∠AFE=∠A'+∠A'DB,再用折叠的性质和直角三角形的性质即可得出结论.
解答 解:(1)∵a∥b,
∴∠AED=∠AGF,
∵∠AGF=∠CGH,
∴∠AED=∠CGH,
∵∠ACB=90°,
∴∠CGH+∠BH∠=90°,
∴∠AED+∠NHF=90°.
(2)∠AED+∠BHF=90°,
理由:如图2,延长BC,DE交于点G,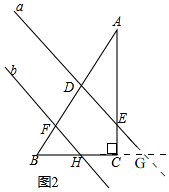
∵∠ACB=90°,
∴∠CGE+∠CEG=90°,
∵∠AED=∠CEG,
∴∠AED+∠CGE=90°,
∵a∥b,
∴∠BHF=∠CGE,
∴∠AED+∠BHF=90°,
故答案为:∠AED+∠BHF=90°.
(3)如图3,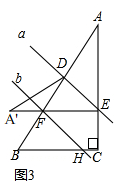
∵A′E∥BC,
∴∠AFE=∠B,
∵∠AFE=∠A'+∠A'DB,
∴∠B=∠A'+∠A'DB,
由折叠得,∠A'=∠A,
∴∠B=∠A+∠A'DB,
∵∠A+∠B=90°,
∴∠B=90°-∠B+∠A'DB,
∴2∠B+∠A'DB=90°.
点评 此题是几何变换综合题,主要考查了平行线的性质,直角三角形的性质,折叠的性质,三角形的外角的性质,解本题的关键用三角形的外角得出∠AFE=∠A'+∠A'DB,是一道比较简单的中考常考题.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
10.室内温度10℃,室外温度是-3℃,那么室内温度比室外温度高( )
| A. | 13℃ | B. | 7℃ | C. | -7℃ | D. | -13℃ |
12.如图图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第10个图案中白色正方形的个数为( )
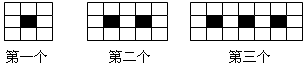

| A. | 50 | B. | 53 | C. | 55 | D. | 60 |
18.已知a+b=1,ab=3,则a2+b2-ab的值为( )
| A. | -2 | B. | -8 | C. | 10 | D. | -10 |