题目内容
9.若点P(a,b)在直线y=-x+5上,又在双曲线$y=\frac{3}{x}$上,则a2b+ab2=15.分析 把点P(a,b)分别代入y=-x+5,$y=\frac{3}{x}$,求得a+b=5,ab=3,由a2b+ab2=ab(a+b),整体代入即可求得.
解答 解:把点P(a,b)代入y=-x+5得,b=-a+5,
则a+b=5,
把点P(a,b)代入$y=\frac{3}{x}$得,b=$\frac{3}{a}$,则ab=3,
所以a2b+ab2=ab(a+b)=3×5=15.
故答案为15.
点评 本题考查了反比例函数图象上点的坐标特征,一次函数图象上点的坐标特征,求得a+b=5,ab=3是本题的关键.

练习册系列答案
相关题目
19.如果m=$\sqrt{10}$-1,那么m的取值范围是( )
| A. | 0<m<1 | B. | 1<m<2 | C. | 2<m<3 | D. | 3<m<4 |
1.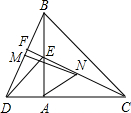 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点A,D,C在同一直线上,直线CE交BD于F,连接AF,点M,N分别是BD,CE的中点,有下列说法:①BD=CE;②CF⊥BD;③AF平分∠DFC;④△AMN是等腰直角三角形.其中正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点A,D,C在同一直线上,直线CE交BD于F,连接AF,点M,N分别是BD,CE的中点,有下列说法:①BD=CE;②CF⊥BD;③AF平分∠DFC;④△AMN是等腰直角三角形.其中正确的结论有( )
 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点A,D,C在同一直线上,直线CE交BD于F,连接AF,点M,N分别是BD,CE的中点,有下列说法:①BD=CE;②CF⊥BD;③AF平分∠DFC;④△AMN是等腰直角三角形.其中正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点A,D,C在同一直线上,直线CE交BD于F,连接AF,点M,N分别是BD,CE的中点,有下列说法:①BD=CE;②CF⊥BD;③AF平分∠DFC;④△AMN是等腰直角三角形.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.在直角坐标系中,点P落在直线x-2y+6=0上,O为坐标原点,则|OP|的最小值为( )
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $3\sqrt{5}$ | C. | $\frac{{6\sqrt{5}}}{5}$ | D. | $\sqrt{10}$ |
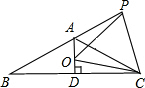 已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,