题目内容
3.在△ABC中,若∠A和∠B均为锐角,且满足等式|2sinA-$\sqrt{3}$|+(tanB-1)2=0.则∠C的度数是75°.分析 先根据非负数的性质求出sinA,tanB的值.再由特殊角的三角函数值求出∠A,∠B的度数,根据三角形内角和定理即可得出∠C的值.
解答 解:∵|2sinA-$\sqrt{3}$|+(tanB-1)2=0,
∴|2sinA-$\sqrt{3}$|=0,(tanB-1)2=0,
∴sinA=$\frac{\sqrt{3}}{2}$,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°-60°-45°=75°.
故答案为:75°.
点评 本题考查的是特殊角的三角函数值,熟记各特殊角的三角函数值是解答此题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
13.既是分数又是正有理数的是( )
| A. | +2 | B. | -$\frac{3}{5}$ | C. | 0 | D. | 2.015 |
11.请你观察下面的四个图形,它们体现了中华民族的传统文化.

对称现象无处不在,其中可以看作是轴对称图形的有( )

对称现象无处不在,其中可以看作是轴对称图形的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.用科学记数法表示的数-3.2×10-4写成小数是( )
| A. | 0.00032 | B. | -0.0032 | C. | -0.00032 | D. | -32000 |
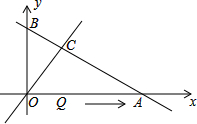 如图,直线y=-$\frac{1}{2}$x+3与坐标轴分别交于点A、B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连接CQ.若△OQC是等腰直角三角形,则t的值为2或4.
如图,直线y=-$\frac{1}{2}$x+3与坐标轴分别交于点A、B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连接CQ.若△OQC是等腰直角三角形,则t的值为2或4.