题目内容
4.计算:${({-\sqrt{3}})^2}+({\sqrt{2015}-\sqrt{2016}})({\sqrt{2016}+\sqrt{2015}})-2|{\sqrt{\frac{1}{2}}-{{tan}^{-1}}{{45}°}}|$.分析 先利用负整数指数幂的意义和平方差公式、特殊角的三角函数值得到原式=3+(2015-2016)-2|$\frac{\sqrt{2}}{2}$-1|,然后去绝对值后合并即可.
解答 解:原式=3+(2015-2016)-2|$\frac{\sqrt{2}}{2}$-1|
=3-1+2($\frac{\sqrt{2}}{2}$-1)
=2+$\sqrt{2}$-2
=$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了负整数指数幂.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
16. 如图,两条宽为1的带子,相交成α角,那么重叠部分的面积即阴影部分的面积为( )
如图,两条宽为1的带子,相交成α角,那么重叠部分的面积即阴影部分的面积为( )
 如图,两条宽为1的带子,相交成α角,那么重叠部分的面积即阴影部分的面积为( )
如图,两条宽为1的带子,相交成α角,那么重叠部分的面积即阴影部分的面积为( )| A. | sinα | B. | $\frac{1}{sinα}$ | C. | $\frac{1}{si{n}^{2}α}$ | D. | $\frac{1}{cosα}$ |
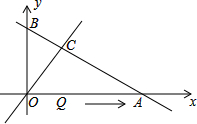 如图,直线y=-$\frac{1}{2}$x+3与坐标轴分别交于点A、B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连接CQ.若△OQC是等腰直角三角形,则t的值为2或4.
如图,直线y=-$\frac{1}{2}$x+3与坐标轴分别交于点A、B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连接CQ.若△OQC是等腰直角三角形,则t的值为2或4. 如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(5,0),则点A的坐标为(2.5,5).
如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(5,0),则点A的坐标为(2.5,5). 已知一次函数图象如图,则它的表达式为y=2x-2.
已知一次函数图象如图,则它的表达式为y=2x-2.