题目内容
5.对于二次函数f(x)=ax2-bx+c,当a>0时,只有最小值为$\frac{4ac-{b}^{2}}{4a}$,这个结论一定正确吗?分析 直接利用配方法求出二次函数的顶点式,即可求得出二次函数的顶点坐标,根据二次函数的性质求得出二次函数的最小值.
解答 解:对于二次函数f(x)=ax2-bx+c,当a>0时,只有最小值为$\frac{4ac-{b}^{2}}{4a}$,这个结论一定正确;
∵二次函数f(x)=ax2-bx+c
=a(x-$\frac{b}{2a}$)2+$\frac{4ac-{b}^{2}}{4a}$;
∴图象的顶点坐标为:($\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),
∵a>0,
∴函数的最小值为:$\frac{4ac-{b}^{2}}{4a}$.
点评 此题主要考查了求二次函数的最值,熟练掌握二次函数的性质是解题关键.

练习册系列答案
相关题目
1. 如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )
如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )
 如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )
如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )| A. | 20° | B. | 60° | C. | 70° | D. | 80° |
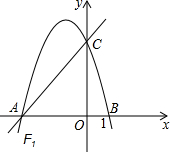 如图,直线y=$\frac{4}{3}$x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
如图,直线y=$\frac{4}{3}$x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).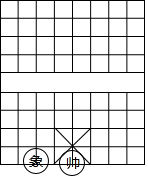 如图,中国象棋中对“象”的走法有一定的限制,只能走“田”字.若此时“象”的坐标为(-2,-4)“帅”的坐标为(0,-4),试写出此“象”下一步可能走到的各位置的坐标.
如图,中国象棋中对“象”的走法有一定的限制,只能走“田”字.若此时“象”的坐标为(-2,-4)“帅”的坐标为(0,-4),试写出此“象”下一步可能走到的各位置的坐标.