题目内容
15.当|x-2|+|x-3|取最小值时,请求出|x-2|+|x-3|-|x-1|的最小值和最大值.分析 |x-2|+|x-3|是数轴上,到2、3两点的距离之和,其最小值为1,则2≤x≤3,在|x-2|+|x-3|-|x-1|中,|x-2|+|x-3|是定值为1,所以|x-1|的值最小时,原式的值最大,当|x-1|的值最大时,原式的值最小.
解答 解:由题意得:当|x-2|+|x-3|取最小值时,2≤x≤3,
当x=2时,|x-2|+|x-3|-|x-1|是最大值,
|x-2|+|x-3|-|x-1|=1-|2-1|=0,
当x=3时,|x-2|+|x-3|-|x-1|是最小值,
|x-2|+|x-3|-|x-1|=1-|3-1|=-1,
所以|x-2|+|x-3|-|x-1|的最小值是-1,最大值是0.
点评 本题是绝对值的最值问题,难度较大,考查了绝对值和数轴上两点的距离的关系,熟练掌握:若数轴上点A表示的数为x,点B表示的数为y时,AB=|x-y|.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
3.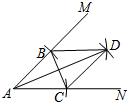 如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于$\frac{1}{2}$BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )
如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于$\frac{1}{2}$BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )
 如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于$\frac{1}{2}$BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )
如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于$\frac{1}{2}$BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )| A. | AD平分∠MAN | B. | AD垂直平分BC | ||
| C. | ∠MBD=∠NCD | D. | 四边形ACDB一定是菱形 |
10.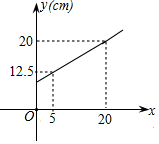 弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是( )
弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是( )
 弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是( )
弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是( )| A. | 9cm | B. | 10cm | C. | 10.5cm | D. | 11cm |
4.单项式-$\frac{{2}^{3}{a}^{2}b}{5}$的次数是( )
| A. | -23 | B. | -$\frac{8}{5}$ | C. | 6 | D. | 3 |
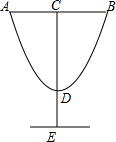 设计师以y=2x2-4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=11.
设计师以y=2x2-4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=11. 一条排水管的截面如图所示.已知排水管的半径OB=10,水面宽AB=16.求截面圆心O到水面的距离.
一条排水管的截面如图所示.已知排水管的半径OB=10,水面宽AB=16.求截面圆心O到水面的距离.