题目内容
17．为选拔一名选手参加全国中学生游泳锦标赛自由泳比赛，我市四名中学生参加了男子100米自由泳训练，他们成绩的平均数$\overline{x}$及其方差s2如下表所示：| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 1′05″33 | 1′04″26 | 1′04″26 | 1′07″29 |
| S2 | 1.1 | 1.1 | 1.3 | 1.6 |
分析 首先比较平均数，平均数相同时选择方差较小的运动员参加．
解答 解：∵$\overline{{x}_{丁}}$＞$\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$=$\overline{{x}_{丙}}$，
∴从乙和丙中选择一人参加比赛，
∵S${{\;}_{乙}}^{2}$＜S${{\;}_{丙}}^{2}$，
∴选择乙参赛，
故答案为：乙．
点评 题考查了平均数和方差，一般地设n个数据，x1，x2，…xn的平均数为$\overline{x}$，则方差S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
练习册系列答案
相关题目
7．
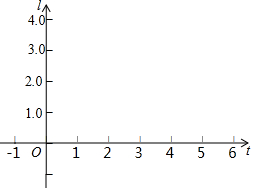某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中，电动伸缩门伸缩后的总长度1（米）与按电钮开关的时间t（秒）之间存在某种函数关系（电动伸缩门初始状态是完全收拢的）．经几次试验后，得到一组对应数据如下：
（1）请你在已建立的平面直角坐标系中，通过①描点、连线，②猜测l与t之间的函数关系，③求出函数的解析式，④验证，这四个步骤确定l与t之间的函数关系；
（2）已知学校的大门宽为5米，问将校门完全关闭再完全打开共用多少秒？
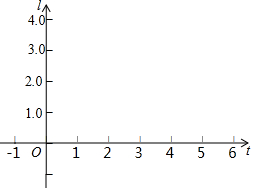某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中，电动伸缩门伸缩后的总长度1（米）与按电钮开关的时间t（秒）之间存在某种函数关系（电动伸缩门初始状态是完全收拢的）．经几次试验后，得到一组对应数据如下：| t（秒） | 0 | 1 | 2 | 3 | 4 | 5 | … |
| l（米） | 1 | 1.4 | 1.8 | 2.2 | 2.6 | 3.0 | … |
（2）已知学校的大门宽为5米，问将校门完全关闭再完全打开共用多少秒？
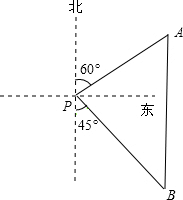如图，一艘海轮位于灯塔P的北偏东60°方向，距离灯塔86n mile的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，此时，B处与灯塔P的距离约为102n mile．（结果取整数，参考数据：$\sqrt{3}$≈1.7，$\sqrt{2}$≈1.4）
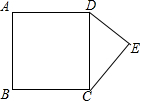如图，以正方形ABCD的边CD为斜边向外作Rt△CDE，若DE=5且点A到CE的距离为17，则CD=13．
9．从一副洗匀的普通扑克牌中随机抽取一张，则抽出红桃的概率是（ ）
| A． | $\frac{1}{54}$ | B． | $\frac{13}{54}$ | C． | $\frac{1}{13}$ | D． | $\frac{1}{4}$ |