题目内容
14.因式分解:(1)3x(x-2)-(2-x);
(2)4q(1-p)3+2(p-1)2;
(3)-4m2n2+12m3n2-2mn;
(4)a2xn+2+abxn+1-acxn-adxn-1(n为正整数);
(5)a(a-b)3+2a2(b-a)2-2ab(b-a)2;
(6)3xy(a-b)2+9x(b-a);
(7)(2x-1)y2+(1-2x)3y;
(8)a2(a-1)2-a(1-a)2.
分析 (1)原式变形后,提取公因式即可得到结果;
(2)原式变形后,提取公因式即可得到结果;
(3)原式提取公因式即可得到结果;
(4)原式提取公因式即可得到结果;
(5)原式变形后,提取公因式即可得到结果;
(6)原式变形后,提取公因式即可得到结果;
(7)原式变形后,提取公因式即可得到结果;
(8)原式变形后,提取公因式即可得到结果.
解答 解:(1)原式=3x(x-2)+(x-2)=(x-2)(3x+1);
(2)原式=-4q(p-1)3+2(p-1)2=2(p-1)2(-2qp+2q+1);
(3)原式=-2mn(-2mn-6m2n+1);
(4)原式=axn-1(ax3+bx2-cx-d);
(5)原式=a(a-b)2(a-b+2a2-2ab);
(6)原式=3x(a-b)(ay-by-9x);
(7)原式=(2x-1)y[y-(2x-1)2];
(8)原式=a(a-1)2(a-1)=a(a-1)3.
点评 此题考查了提公因式与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
2.在一个圆中任画六条半径,可以把这个圆分割成扇形的个数为( )
| A. | 14 | B. | 18 | C. | 30 | D. | 36 |
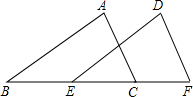 △ABC≌△DEF,AC与DF是对应边,∠A与∠D是对应角.
△ABC≌△DEF,AC与DF是对应边,∠A与∠D是对应角.