题目内容
16.解方程(或组)(1)$\left\{\begin{array}{l}{x=1-y}\\{2x-y+4=0}\end{array}$
(2)$\left\{\begin{array}{l}{2x-5y=9}\\{\frac{x+y}{3}=\frac{x-y}{2}+1}\end{array}$
(3)$\left\{\begin{array}{l}{3x+4z=7}\\{2x+3y+z=9}\\{x-y+z=8}\end{array}$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可;
(3)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x=1-y①}\\{2x-y+4=0②}\end{array}\right.$,
把①代入②得:2-2y-y+4=0,即y=2,
把y=2代入①得:x=-1,
则方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{2x-5y=9①}\\{x-5y=-6②}\end{array}\right.$,
①-②得:x=15,
把x=15代入②得:y=$\frac{21}{5}$,
则方程组的解为$\left\{\begin{array}{l}{x=15}\\{y=\frac{21}{5}}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{3x+4z=7①}\\{2x+3y+z=9②}\\{x-y+z=8③}\end{array}\right.$,
②+③×3得:5x+4z=33④,
④-①得:2x=26,即x=13,
把x=13代入①得:z=-8,
把x=13,z=-8代入③得:y=-3,
则方程组的解为$\left\{\begin{array}{l}{x=13}\\{y=-3}\\{z=-8}\end{array}\right.$.
点评 此题考查了解二元一次方程组,以及解三元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{ax+by=8}\\{bx-ay=1}\end{array}\right.$的解,则4a-5b的平方根为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | ±$\sqrt{2}$ | D. | ±2 |
1.下列从左到右的变形中,属于因式分解的是( )
| A. | (x+y)(x-2y)=x2-xy+y2 | B. | 3x2-x=x(3x-1) | ||
| C. | (a-b)2=(a-b)(a-b) | D. | m2-n2=(m-n)2 |
8.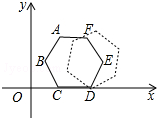 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(50,2)的是( )
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(50,2)的是( )
 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(50,2)的是( )
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(50,2)的是( )| A. | 点A | B. | 点B | C. | 点 C | D. | 点D |
6.4的平方根是( )
| A. | ±16 | B. | 2 | C. | ±2 | D. | ±$\sqrt{2}$ |