题目内容
2．
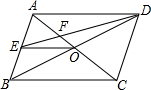如图，O为?ABCD的对角线交点，E为AB的中点，DE交AC于点F，若S四边形ABCD=12，则S△BOE的值为$\frac{3}{2}$．
分析 由O为?ABCD的对角线交点，E为AB的中点，可得OE是△ABD的中位线，即可证得△BOE∽△BDA，然后由相似三角形面积比等于相似比的平方，求得答案．
解答 解：∵O为?ABCD的对角线交点，
∴OB=OD，
∵E为AB的中点，
∴OE∥AD，
∴△BOE∽△BDA，
∴S△BOE：S△ABD=（$\frac{OB}{BD}$）2=1：4，
∵S四边形ABCD=12，
∴S△ABD=$\frac{1}{2}$S四边形ABCD=6，
∴S△BOE=$\frac{3}{2}$．
故答案为：$\frac{3}{2}$．
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质．注意证得△BOE∽△BDA是解此题的关键．
练习册系列答案
相关题目
