题目内容
12.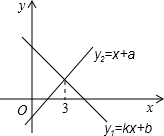 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③不等式kx+b<x+a的解集为x<3中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③不等式kx+b<x+a的解集为x<3中,正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据一次函数的性质对①②进行判断;根据一次函数与一元一次不等式的关系,利用两函数图象的位置对③进行判断.
解答 解:∵一次函数y1=kx+b的图象经过第二、四象限,
∴k<0,所以①正确;
∵一次函数y2=x+a的图象与y轴的交点在x轴下方,
∴a<0,所以②错误;
∵x>3时,一次函数y1=kx+b的图象都在函数y2=x+a的图象下方,
∴不等式kx+b<x+a的解集为x>3,所以③错误.
故选B.
点评 本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.也考查了一次函数的图象与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.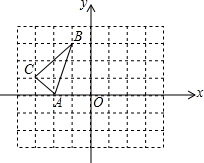 如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
 如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )| A. | (1,-1) | B. | (1,1) | C. | (-1,1) | D. | (-1,-1) |
1.向量($\overrightarrow{AB}$+$\overrightarrow{MB}$)+($\overrightarrow{BO}$+$\overrightarrow{BC}$)+$\overrightarrow{OM}$化简后的结果等于( )
| A. | $\overrightarrow{BC}$ | B. | $\overrightarrow{AB}$ | C. | $\overrightarrow{AC}$ | D. | $\overrightarrow{AM}$ |
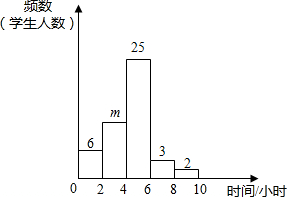 分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题: 已知一次函数与反比例函数的图象交于P(-3,m),Q(2,-3).
已知一次函数与反比例函数的图象交于P(-3,m),Q(2,-3).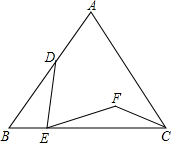 如图,在等边△ABC中,D、E分别为AB、BC边上的动点,满足AD=2BE,将线段DE绕点E顺时针旋转60°得线段EF,求证:CF平分∠ACB.
如图,在等边△ABC中,D、E分别为AB、BC边上的动点,满足AD=2BE,将线段DE绕点E顺时针旋转60°得线段EF,求证:CF平分∠ACB.