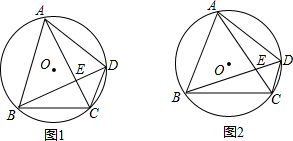题目内容
19.(1)尝试探究如图1,Rt△ABC中,AB=AC,AD是高,点E是AB边上一点,CE与AD交于点G,过点E作EF⊥CE交BC于点F.若AE=2BE,则EF与EG的数量关系是EG=2EF.
(2)类比延伸
如图2,在(1)的条件下,若AE=nBE(n>0),则EF与EG的数量关系是EG=nEF(用含n的代数式表示),试写出解答过程.
(3)拓展迁移
如图3,Rt△ABC中,∠BAC=90°,AD是高,点E是AB边上一点,CE与AD交于点G,过点E作EF⊥CE交BC于点F,若AE=aBE,AB=bAC(a>0,b>0),则EF与EG的数量关系是EG=abEF.
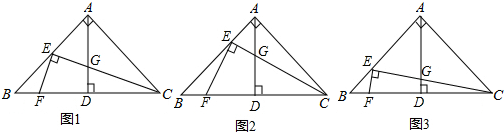
分析 (1)如图1中,过点E分别作EP⊥BD于点P,作EQ⊥AD于点Q,先证明△BPE∽△AQE,再证明△EPF∽△EQG即可.
(2)如图2中,过点E分别作EP⊥BD于点P,作EQ⊥AD于点Q,证明方法类似(1).
(3)如图3中,过点E分别作EP⊥BD于点P,作EQ⊥AD于点Q,由△EPF∽△EQG,得$\frac{AE}{BE}$=$\frac{AQ}{EP}$ ①,由△AEQ∽△CBA,得$\frac{AB}{AC}$=$\frac{EQ}{AQ}$ ②,①×②得$\frac{EQ}{EP}$=ab,由此即可解决问题.
解答 解:(1)EG=2EF;
理由:如图1中,过点E分别作EP⊥BD于点P,作EQ⊥AD于点Q.
∴∠BPE=∠AQE=90°.
∵AD是等腰直角三角形的高,
∴∠B=∠EAQ=45°.
∴△BPE∽△AQE,
∴$\frac{EP}{EQ}$=$\frac{BE}{AE}$=$\frac{1}{2}$,
∴EQ=2EP,
∵∠FEP+∠PEG=90°,∠GEQ+∠PEG=90°,
∴∠FEP=∠GEQ.
又∵∠EPF=∠EQG=90°,
∴△EPF∽△EQG,
∴$\frac{EP}{EQ}$=$\frac{EF}{EG}$=$\frac{1}{2}$,
∴EG=2EF.
故答案为EG=2EF.
(2)EG=nEF;
理由:如图2中,过点E分别作EP⊥BD于点P,作EQ⊥AD于点Q.
∴∠BPE=∠AQE=90°.
∵AD是等腰直角三角形的高,
∴∠B=∠EAQ=45°.
∴△BPE∽△AQE,
∴$\frac{EP}{EQ}$=$\frac{BE}{AE}$,
∵AE=nBE,
∴EQ=nEP.
∵∠FEP+∠PEG=90°,∠GEQ+∠PEG=90°,
∴∠FEP=∠GEQ.
又∵∠EPF=∠EQG=90°,
∴△EPF∽△EQG,
∴$\frac{EP}{EQ}$=$\frac{EF}{EG}$,
∴EG=nEF.
故答案为EG=2EF.
(3)EG=abEF,
理由:如图3中,过点E分别作EP⊥BD于点P,作EQ⊥AD于点Q,
∵△EPF∽△EQG,
∴$\frac{AE}{BE}$=$\frac{AQ}{EP}$ ①
∵∠AQE=∠BAC,∠EAQ=∠ACB,
∴△AEQ∽△CBA,
∴$\frac{AQ}{AC}$=$\frac{EQ}{AB}$,
∴$\frac{AB}{AC}$=$\frac{EQ}{AQ}$ ②
①×②得$\frac{AE}{BE}$•$\frac{AB}{AC}$=$\frac{EQ}{EP}$=ab,
∵△EPF∽△EQG,
∴$\frac{EP}{EQ}$=$\frac{EF}{EG}$,
∴$\frac{EG}{EF}$=ab,
∴EG=abEF.
故答案为EG=abEF.
点评 本题考查相似三角形的判定和性质,解题的关键是添加辅助线,构造相似三角形,本题需要用到多次相似,属于中考常考题型.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
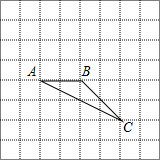 如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.