题目内容
9.观察式子:(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1;
(x-1)(x4+x3+x2+x+1)=x5-1;
…
你能得出一般情况下(x-1)(xn-1+xn-2+…+x2+x+1)的结果吗?并根据这一结果计算1+2+22+…+248.
分析 仔细观察上式就可以发现得数中x的指数是式子中x的最高指数加1,根据此规律就可求出本题.
解答 解:(1)(x-1)(xn-1+xn-2+xn-3+…+x+1)=xn-1;
(2)1+2+22+23+24+…+248
=(2-1)(1+2+22+23+24+…+229+248)
=249-1.
点评 考查了多项式乘多项式,本题主要锻炼学生从已知的题中找规律.所以学生平时要注意培养自己的总结概括能力.

练习册系列答案
相关题目
17.据四川新闻网3月3日报道,成都地铁春运至今(2013年3月3日止),成都地铁运送乘客21600000人次,用科学记数法表示为( )
| A. | 2.16×108人 | B. | 2.16×107人 | C. | 0.216×108人 | D. | 216×105人 |
4.下列各式计算正确的是( )
| A. | (-5an+1b)(-2a)=-10an+2b | B. | (-4a2b)(-a2b2)($\frac{1}{2}$b3c)=2a4b6c | ||
| C. | (-3xy)(-x2z)6xy2=3x3y3z | D. | (2anb3)(-$\frac{1}{6}$abn-1)=-$\frac{1}{3}$an+1b3n-3 |
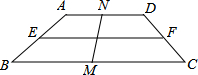 如图,在梯形ABCD中AD∥BC,∠B=40°,∠C=50°,E、M、F、N分别是边AB、BC、CD、DA的中点,且EF=a,MN=b,则BC的长为a+b.
如图,在梯形ABCD中AD∥BC,∠B=40°,∠C=50°,E、M、F、N分别是边AB、BC、CD、DA的中点,且EF=a,MN=b,则BC的长为a+b. 如图,在四边形ABCD中,AB=BC=2,CD=4,DA=2$\sqrt{2}$,且∠B=90°,求∠DAB的度数.
如图,在四边形ABCD中,AB=BC=2,CD=4,DA=2$\sqrt{2}$,且∠B=90°,求∠DAB的度数.