题目内容
17.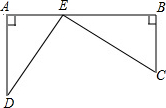 如图,铁路上A、B两站相距25km,C,D为两村庄,且DA⊥AB,CB⊥AB,已知AD=15km,CB=10km,在AB上是否存在一点E,使它到C、D两村庄的距离相等?若存在,求出此时AE的距离;若不存在,请说明理由.
如图,铁路上A、B两站相距25km,C,D为两村庄,且DA⊥AB,CB⊥AB,已知AD=15km,CB=10km,在AB上是否存在一点E,使它到C、D两村庄的距离相等?若存在,求出此时AE的距离;若不存在,请说明理由.
分析 由勾股定理两直角边的平方和等于斜边的平方即可求,即在直角三角形DAE和直角三角形CBE中,DE2=AD2+AE2,CE2=BE2+BC2,AD2+AE2=BE2+BC2,设AE为x,则BE=25-x,将BC=10代入关系式即可求得.
解答 解:∵C、D两村到E站距离相等,∴CE=DE,
在Rt△DAE和Rt△CBE中,DE2=AD2+AE2,CE2=BE2+BC2,
∴AD2+AE2=BE2+BC2.
设AE为x,则BE=25-x,
将BC=10,DA=15代入关系式为x2+152=(25-x)2+102,
整理得,50x=500,
解得x=10,
∴E站应建在距A站10km处.
点评 本题主要是运用勾股定理将两个直角三角形的斜边表示出来,两边相等求解即可,解题的关键是根据不同的两个直角三角形有相等的斜边列出等式求解.

练习册系列答案
相关题目
9. 如图①,是小明把一个梯形图沿对称轴剪开拼成图②,其中a>b.则由图①到图②能验证的公式是( )
如图①,是小明把一个梯形图沿对称轴剪开拼成图②,其中a>b.则由图①到图②能验证的公式是( )
 如图①,是小明把一个梯形图沿对称轴剪开拼成图②,其中a>b.则由图①到图②能验证的公式是( )
如图①,是小明把一个梯形图沿对称轴剪开拼成图②,其中a>b.则由图①到图②能验证的公式是( )| A. | (a+b)(a-b)=a2-b2 | B. | a2-b2=(a-b)(a+b) | C. | (a-b)2=a2-2ab+b2 | D. | a2-2ab+b2=(a-b)2 |
7.下列运算正确的是( )
| A. | $\sqrt{4}$=2 | B. | (-3)2=-9 | C. | 2-3=-6 | D. | 20=0 |
 如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种地毯每平方米售价20元,主楼梯宽2米.则购地毯至少需要280元.
如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种地毯每平方米售价20元,主楼梯宽2米.则购地毯至少需要280元.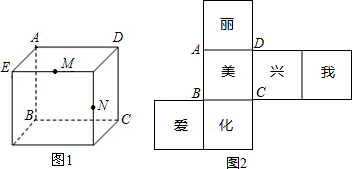
 如图,已知O为直线AF上一点,OE平分∠AOC,
如图,已知O为直线AF上一点,OE平分∠AOC,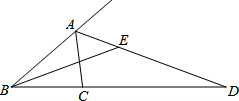 在△ABC中,∠ACB=2∠B,AD为△ABC的外角平分线交射线BC于点D,作∠ABC的角平分线交AD于点E.若CD=5,AC=2,则tan∠AEB=$\frac{\sqrt{3}}{3}$.
在△ABC中,∠ACB=2∠B,AD为△ABC的外角平分线交射线BC于点D,作∠ABC的角平分线交AD于点E.若CD=5,AC=2,则tan∠AEB=$\frac{\sqrt{3}}{3}$.