题目内容
16．若α为锐角，且sinα=$\frac{4}{5}$，则tanα为（ ）| A． | $\frac{9}{25}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
分析 根据同角三角函数的关系，可得α余弦，根据正弦、余弦、正切的关系，可得答案．
解答 解：由α为锐角，且sinα=$\frac{4}{5}$，得
cosα=$\sqrt{1-si{n}^{2}α}$=$\sqrt{1-（\frac{4}{5}）^{2}}$=$\frac{3}{5}$，
tanα=$\frac{sinα}{cosα}$=$\frac{\frac{4}{5}}{\frac{3}{5}}$=$\frac{4}{3}$，
故选：D．
点评 本题考查了同角三角函数的关系，利用了sin2α+cos2α=1，tanα=$\frac{sinα}{cosα}$．
练习册系列答案
相关题目
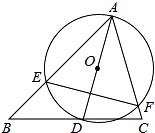如图，∠BAC=60°，∠ABC=45°，AB=4$\sqrt{2}$，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连接EF，则线段EF长度的最小值为2$\sqrt{3}$．
如图，某宾馆在重新装修后，准备在大厅的主楼梯上铺上红色地毯，已知这种地毯每平方米售价20元，主楼梯宽2米．则购地毯至少需要280元．