题目内容
8.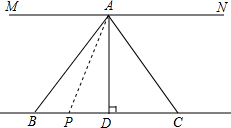 已知:如图,AD平分∠BAC,且AD⊥BC于点D,MN∥BC,请在括号中补全步骤的推理理由.
已知:如图,AD平分∠BAC,且AD⊥BC于点D,MN∥BC,请在括号中补全步骤的推理理由.(1)试说明∠BAM=∠CAN.
∵MN∥BC,( )
∴∠BAM=∠ABC,∠CAN=∠ACB.( )
又∵AD⊥BC,( )
∴∠ADB=∠ADC=90°,( )
∴∠BAD+∠ABC=90°,∠CAD+∠ACB=90°,
又∵AD平分∠BAC,( )
∴∠BAD=∠CAD,( )
∴∠ABC=∠ACB,( )
∴∠BAM=∠CAN,( )
(2)如果AD=5cm,点P是直线BC上的一个动点,连接AP,则AP不小于5cm.
∵AD⊥BC,AD=5cm,
∴AP≥5cm.( )
分析 (1)先根据平行线的性质得出∠BAM=∠ABC,∠CAN=∠ACB,再由垂直的定义得出∠ADB=∠ADC=90°,故∠BAD+∠ABC=90°,∠CAD+∠ACB=90°,根据AD平分∠BAC可知∠BAD=∠CAD,故可得出∠ABC=∠ACB,由此得出结论;
(2)根据垂线段最短即可得出结论.
解答 解:(1)∠BAM=∠CAN,
∵MN∥BC,(已知)
∴∠BAM=∠ABC,∠CAN=∠ACB.(两直线平行,内错角相等)
又∵AD⊥BC,(已知)
∴∠ADB=∠ADC=90°,(垂直的定义)
∴∠BAD+∠ABC=90°,∠CAD+∠ACB=90°,
又∵AD平分∠BAC,(已知)
∴∠BAD=∠CAD,(角平分线的定义)
∴∠ABC=∠ACB,(等角的余角相等,或等式的性质)
∴∠BAM=∠CAN,(等量代换)
(2)如果AD=5cm,点P是直线BC上的一个动点,连接AP,则AP不小于5cm.
∵AD⊥BC,AD=5cm,
∴AP≥5cm(垂线段最短).
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
相关题目
18.已知二次函数y=ax2+bx+c(a≠0)与x轴的交点坐标为A(m,0),B(n,0),点A在点B的左边,当ax2+bx+c=2015时有实数根x1,x2(x1<x2),以下说法中不正确的是( )
| A. | 当a>0时,x1<m<n<x2 | |
| B. | 当a<0时,m<x1<x2<n | |
| C. | 存在m+n=x1+x2 | |
| D. | y=ax2+bx+c-2015与x轴的交点坐标不可能是(x1,0),(x2,0) |
19.小明购买文具一共要付32元,小明钱包里只有2元和5元两种面值若干张钱,他一共有几种不同的付款方案( )
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
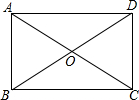 如图,在矩形ABCD中,两条对角线AC、BD相交于点O,AB=OA=4cm,求BD与AD的长.
如图,在矩形ABCD中,两条对角线AC、BD相交于点O,AB=OA=4cm,求BD与AD的长.