题目内容
5.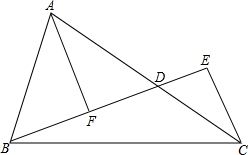 在锐角△ABC中,在AC上取一点D,使得AB=AD,连接BD,过点C作CE⊥BD,交BD的延长线于点E,过点A作AF⊥BD,交BD于点F,如图所示,若∠ACB=∠BAF,DE=4,则点D到BC的距离为4.
在锐角△ABC中,在AC上取一点D,使得AB=AD,连接BD,过点C作CE⊥BD,交BD的延长线于点E,过点A作AF⊥BD,交BD于点F,如图所示,若∠ACB=∠BAF,DE=4,则点D到BC的距离为4.
分析 分析:过点D作DG⊥BC于点G,只要证明DG=DE即可解决问题.
解答  解:过点D作DG⊥BC于点G,
解:过点D作DG⊥BC于点G,
∵AB=AD,AF⊥BD,
∴∠BAF=∠DAF,
又∵∠ACB=∠BAF,
∴∠DAF=∠ACB,
∵CE⊥BD,AF⊥BD,
∴AF∥CE,
∴∠DAF=∠ECD,
∴∠ACB=∠ECD,
∴DG=DE=4(角平分线上的点到这个角两边的距离相等),
∴点D到BC的距离为4.
点评 本题考查的是点到直线距离的定义,象这样的问题一般都要转化为求垂线段长度的问题来求解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
5.下列方程中,有实数解的是( )
| A. | 2x4+1=0 | B. | $\sqrt{x-2}$+3=0 | C. | x2-x+2=0 | D. | $\frac{x}{x-1}$=$\frac{1}{{x}^{2}-1}$ |
10.抛物线y=-3x2+2x-1与y轴的交点为( )
| A. | (0,1) | B. | (0,-1) | C. | (-1,0) | D. | (1,0) |
15. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )| A. | 小明中途休息用了20分钟 | |
| B. | 小明休息前爬山的平均速度为每分钟70米 | |
| C. | 小明休息后爬山的平均速度为每分钟38米 | |
| D. | 小明在上述过程中所走的路程为3800米 |