题目内容
13. 如图,在 Rt△ABC中,∠ACB=90°,AC=BC=6 cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1 cm的速度向终点C运动.当△PQC为等腰三角形时,则t的值为2.
如图,在 Rt△ABC中,∠ACB=90°,AC=BC=6 cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1 cm的速度向终点C运动.当△PQC为等腰三角形时,则t的值为2.
分析 分三种情况:①PQ=PC时,根据等腰直角三角形的性质得出AM=PM,利用等腰三角形的性质得出QN=NC,进而得出BC=3t,即可得出答案;
②PQ=CQ时,得出PQ=PN,不合题意;
③CP=CQ时,得出PC=PN,不合题意;即可得出结论.
解答 解:过点P作PN⊥BC于点N,PM⊥AC于点M,分三种情况:
①PQ=PC时,
则QN=NC,
∵点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,
∴AP=$\sqrt{2}$t,BQ=t,
∵∠BCA=90°,AC=BC=6cm,
∴∠B=∠A=45°,
∴AM=PM=t,
∴BQ=QN=NC=PM=t,
∴BC=3t=6,
解得:t=2.
②当PQ=CQ时,
∵BQ=t,AM=t,
∴PQ=CQ=6-t,PN=CM=6-t,
则PQ=PN,不合题意;
③当CP=CQ时,
∵BQ=t,AM=t,
∴CP=CQ=6-t,PN=CM=6-t,
则PC=PN,不合题意;
综上所述:当△PQC为等腰三角形时,则t的值为2;
故答案为:2.
点评 此题主要考查了等腰直角三角形的性质以及等腰三角形的性质等知识,根据已知用t表示出相关线段是解题关键.

练习册系列答案
相关题目
4.过八边形的一个顶点最多可以引_______条对角线( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
8.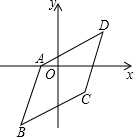 如图,已知?ABCD三个顶点坐标是A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点D的坐标是( )
如图,已知?ABCD三个顶点坐标是A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点D的坐标是( )
 如图,已知?ABCD三个顶点坐标是A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点D的坐标是( )
如图,已知?ABCD三个顶点坐标是A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点D的坐标是( )| A. | (3,1) | B. | (3,2) | C. | (3,3) | D. | (3,4) |
5. 有理数a,b在数轴上的位置如图所示,则下列各式正确的是( )
有理数a,b在数轴上的位置如图所示,则下列各式正确的是( )
 有理数a,b在数轴上的位置如图所示,则下列各式正确的是( )
有理数a,b在数轴上的位置如图所示,则下列各式正确的是( )| A. | -b>0>a | B. | |b|>|a| | C. | |b|<1 | D. | |b|<|a| |
2.∠1与∠2是两条直线被第三条直线所截的同位角,若∠1=50°,则∠2为( )
| A. | 50° | B. | 130° | C. | 50°或130° | D. | 不能确定 |
 如图,直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG移动,直到AB与DC重合时停止,移动前如图①所示,∠B=90°,AB=8cm,BC=6cm,正方形的边长为8cm.设移动x(s)时,三角形与正方形重叠部分的面积y(m2)
如图,直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG移动,直到AB与DC重合时停止,移动前如图①所示,∠B=90°,AB=8cm,BC=6cm,正方形的边长为8cm.设移动x(s)时,三角形与正方形重叠部分的面积y(m2) 如图,一艘军舰位于点A处,在其正南方向有一目标B,在点B的正东方向有一目标C,且AB+BC=3海里,在AC上有一艘补给船D,DC为1海里;军舰从点A出发,向AB,BC方向匀速航行,补给船同时从点D出发,沿垂直于AC方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了几海里?
如图,一艘军舰位于点A处,在其正南方向有一目标B,在点B的正东方向有一目标C,且AB+BC=3海里,在AC上有一艘补给船D,DC为1海里;军舰从点A出发,向AB,BC方向匀速航行,补给船同时从点D出发,沿垂直于AC方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了几海里?