题目内容
1. 如图,一艘军舰位于点A处,在其正南方向有一目标B,在点B的正东方向有一目标C,且AB+BC=3海里,在AC上有一艘补给船D,DC为1海里;军舰从点A出发,向AB,BC方向匀速航行,补给船同时从点D出发,沿垂直于AC方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了几海里?
如图,一艘军舰位于点A处,在其正南方向有一目标B,在点B的正东方向有一目标C,且AB+BC=3海里,在AC上有一艘补给船D,DC为1海里;军舰从点A出发,向AB,BC方向匀速航行,补给船同时从点D出发,沿垂直于AC方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了几海里?
分析 设相遇时补给船航行了x海里,则DE=x海里,由于军舰的速度是补给船的2倍,它们的时间相同,可得EC=3-2x,根据勾股定理可得方程x2+12=(3-2x)2,解方程即可求解.
解答 解:设相遇时补给船航行了x海里,则DE=x海里,
∵军舰的速度是补给船的2倍,它们的时间相同,
∴AB+BE=2x,
∵AB+BC=3,
∴EC=3-2x,
在Rt△CDE中,CD=1,
根据勾股定理可得方程
x2+12=(3-2x)2,
解得:x1=2-$\frac{2\sqrt{3}}{3}$,x2=2+$\frac{2\sqrt{3}}{3}$(不合题意,舍去)
答:相遇时补给船航行了(2-$\frac{2\sqrt{3}}{3}$)海里.
点评 此题考查了勾股定理的应用,一元二次方程的应用,根据是运用勾股定理得到关于x的方程.

练习册系列答案
相关题目
10.关于x的一元二次方程x2+(2m+1)x+m2-1=0有两个不相等的实数根,则m的取值范围是( )
| A. | m≥-$\frac{5}{4}$ | B. | m≤-$\frac{5}{4}$ | C. | m<-$\frac{5}{4}$ | D. | m>-$\frac{5}{4}$ |
9.下列式子中,不是二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{a^2}$ | C. | $\sqrt{a}$ | D. | $\sqrt{\frac{1}{3}}$ |
6.下列事件是必然事件的是( )
| A. | 打开电视机,正在播放《中国好声音》 | |
| B. | 上学路上经过十字路口遇上红灯 | |
| C. | 掷一枚均匀的硬币,正面朝上 | |
| D. | 从1、2、3、4、5这五个数中任取一个数,取到的数一定大于0 |
11.已知直角三角形的周长是2+$\sqrt{6}$,斜边长为 2,则它的面积是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$$\sqrt{6}$ |
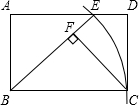 如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交AD边于点E,连接BE,过C点作CF⊥BE,垂足为F
如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交AD边于点E,连接BE,过C点作CF⊥BE,垂足为F 如图所示,∠AOE=90°,∠BOD=45°,那么不大于90°的所有角的度数之和是450度.
如图所示,∠AOE=90°,∠BOD=45°,那么不大于90°的所有角的度数之和是450度. 如图,在 Rt△ABC中,∠ACB=90°,AC=BC=6 cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1 cm的速度向终点C运动.当△PQC为等腰三角形时,则t的值为2.
如图,在 Rt△ABC中,∠ACB=90°,AC=BC=6 cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1 cm的速度向终点C运动.当△PQC为等腰三角形时,则t的值为2.