题目内容
3．任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和，如：23=3+5，33=7+9+11，43=13+15+17+19，…按此规律，若m3分裂后其中有一个奇数是2017，则m的值是（ ）| A． | 46 | B． | 45 | C． | 44 | D． | 43 |
分析 根据题意可知2的立方等于2个连续的奇数相加，3的立方等于三个连续的奇数相加，4的立方等于4个连续的奇数相加，由此可以推测哪个数的立方就是多少个连续的奇数相加，从而可以的m的值．
解答 解：∵23=3+5，33=7+9+11，43=13+15+17+19，…，
2017=2×1009-1，
1009=（2+3+4+…+45）-50，
∴若m3分裂后其中有一个奇数是2017，则m=45，
故选B．
点评 本题考查数字的变化类、有理数的相加，解答本题的关键是明确题意，发现题目中数字的变化规律，求出相应的数字的值．
练习册系列答案
相关题目
如图，在 Rt△ABC中，∠ACB=90°，AC=BC=6 cm，点P从点A出发，沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1 cm的速度向终点C运动．当△PQC为等腰三角形时，则t的值为2．
11．已知直角三角形的周长是2+$\sqrt{6}$，斜边长为 2，则它的面积是（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | $\frac{1}{2}$$\sqrt{6}$ |
18．由以下三边不能组成直角三角形的是（ ）
| A． | 5，13，12 | B． | 2，3，$\sqrt{5}$ | C． | 4，7，5 | D． | 1，$\sqrt{2}$，$\sqrt{3}$ |
如图，在矩形ABCD中，对角线AC，BD相交于点O，∠ACB=30°，则∠AOB的大小为60°．
15．下列计算中，正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{6}$ | B． | $\sqrt{5}+\sqrt{6}=\sqrt{11}$ | C． | $2+\sqrt{2}=2\sqrt{2}$ | D． | $\sqrt{2}+\sqrt{2}=2\sqrt{2}$ |
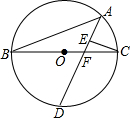如图，BC为⊙O的直径，AB为⊙O的弦，D为$\widehat{BC}$的中点，CE⊥AD于E，AD交BC于点F，tan∠B=$\frac{1}{2}$
13．
如图，在四边形ABCD中，BE⊥AC于点E，连接DE，四边形ABCD的面积为12cm2．若BE平分∠ABC，则四边形ABED的面积为（ ）
如图，在四边形ABCD中，BE⊥AC于点E，连接DE，四边形ABCD的面积为12cm2．若BE平分∠ABC，则四边形ABED的面积为（ ）| A． | 4cm2 | B． | 6cm2 | C． | 8cm2 | D． | 10cm2 |