题目内容
8.解方程:(1)x2+4x=8
(2)x(x+3)=7(x+3)
分析 (1)根据配方法可以解答此方程;
(2)根据提公因式法可以解答此方程.
解答 解:(1)x2+4x=8
x2+4x+4=8+4
(x+2)2=12
∴x+2=$±2\sqrt{3}$
解得,${x}_{1}=-2-2\sqrt{3}$,${x}_{2}=-2+2\sqrt{3}$;
(2)x(x+3)=7(x+3)
x(x+3)-7(x+3)=0
(x-7)(x+3)=0
∴x-7=0或x+3=0
解得,x1=7,x2=-3.
点评 本题考查解一元二次方程-因式分解法,解题的关键是根据方程的特点选择合适的方法解方程.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19.点(5,2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.下列方程中,属于一元二次方程的是( )
| A. | x-y=1 | B. | x=3 | C. | x2-1=0 | D. | 3y-1=0 |
 将如图所示的“点赞”圈案以点O为中心,顺时针旋转90°后得到的图案是( )
将如图所示的“点赞”圈案以点O为中心,顺时针旋转90°后得到的图案是( )



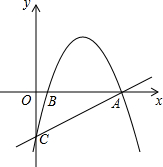 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.