题目内容
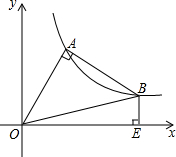 △OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y=
△OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y=| 1 |
| x |
考点:反比例函数综合题
专题:综合题
分析:过点A作AC⊥x轴,过点B做BD⊥AC,利用同角的余角相等得到一对角相等,再由一对直角相等,OA=AB,利用AAS得到三角形AOC与三角形ABD全等,利用全等三角形的对应边相等得到AC=BD,OC=AD,设出A点坐标,表示出BE与OE,即可求出所求式子的值.
解答: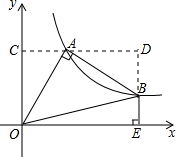 解:过点A作AC⊥x轴,过点B做BD⊥AC,
解:过点A作AC⊥x轴,过点B做BD⊥AC,
∵∠AOC+∠OAC=90°,∠OAC+∠BAD=90°,
∴∠AOC=∠BAD,
在△AOC和△BAD中,
,
∴△AOC≌△BDA(AAS),
∴AC=BD,OC=AD,
由点A在反比例函数y=
上,设A(a,
),
即AC=BD=a,OC=AD=
,
∴BE=DE-BD=
-a,OE=CD=AC+AD=a+
,
∴OE2-BE2=(a+
)2-(
-a)2=4.
故答案为:4.
 解:过点A作AC⊥x轴,过点B做BD⊥AC,
解:过点A作AC⊥x轴,过点B做BD⊥AC,∵∠AOC+∠OAC=90°,∠OAC+∠BAD=90°,
∴∠AOC=∠BAD,
在△AOC和△BAD中,
|
∴△AOC≌△BDA(AAS),
∴AC=BD,OC=AD,
由点A在反比例函数y=
| 1 |
| x |
| 1 |
| a |
即AC=BD=a,OC=AD=
| 1 |
| a |
∴BE=DE-BD=
| 1 |
| a |
| 1 |
| a |
∴OE2-BE2=(a+
| 1 |
| a |
| 1 |
| a |
故答案为:4.
点评:此题属于反比例函数综合题,涉及的知识有:全等三角形的判定与性质,坐标与图形性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列说法中不正确的是( )
| A、6是36的算术平方根 | ||||
B、
| ||||
C、
| ||||
| D、(-3)2的平方根是±3 |
下列说法正确的是( )
| A、同号两数相乘,取原来的符号 |
| B、一个数与-1相乘,积为该数的相反数 |
| C、一个数与0相乘仍得这个数 |
| D、两个数相乘,积大于任何一个乘数 |
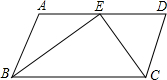 如图,?ABCD中,E为AD的中点,连接BE、CE,∠BEC=90°,求AD与AB的数量关系.
如图,?ABCD中,E为AD的中点,连接BE、CE,∠BEC=90°,求AD与AB的数量关系. 如图,已知PA是⊙O的切线,P为切点,PA=5
如图,已知PA是⊙O的切线,P为切点,PA=5