题目内容
1.已知关于x的一元二次方程mx2-(2m+1)x+2=0(1)求证:此方程总有两个实数根;
(2)若此方程的两个实数根都是整数,求m的整数值;
(3)若a是方程的实数根,求代数式ma3-(4m+1)a2+4(m+1)a+5的值.
分析 (1)根据题意m≠0,则计算判别式有△=(2m-1)2≥0,然后根据判别式的意义即可得到结果;
(2)可先用求根公式表示出两根,再根据方程的根都是整数,可求得m的值;
(3)根据一元二次方程的解的定义得到ma2-(2m+1)a+2=0,变形为ma3-(2m+1)a2+2a=0,然后把所求的代数式变形后利用整体代入的方法进行计算.
解答 (1)证明:∵方程mx2-(2m+1)x+2=0是关于x的一元二次方程,
∴m≠0,
∵△=(2m+1)2-4m×2=(2m-1)2≥0,
∴此方程总有两个实数根;
(2)解:x=$\frac{(2m+1)±\sqrt{(2m+1)^{2}-4m×2}}{2m}$,
∴x1=2,x2=$\frac{1}{m}$.
当m为整数1或-1时,x2为整数,即该方程的两个实数根都是整数,
∴m的值为1或-1,
(3)解:∵a是方程的实数根,
∴ma2-(2m+1)a+2=0,
∴ma3-(2m+1)a2+2a=0,
∴ma3=(2m+1)a2-2a代入ma3-(4m+1)a2+4(m+1)a+5得,
∴(2m+1)a2-2a-(4m+1)a2+4(m+1)a+5=-2ma2+(4m+2)a-4+9
=-2[ma2-(2m-1)a+2]+9=9.
点评 本题主要考查一元二次方程根的判别式,掌握一元二次方程根的判别式与一元二次方程根的情况是解题的关键,即△>0?方程有两个不相等的实数根,△=0?方程有两个相等的实数根,△<0?方程无实数根.

练习册系列答案
相关题目
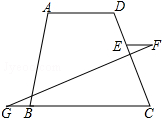 已知∠F=∠G,∠FEC+∠ADC=180°,试判断AD∥BC吗?为什么?
已知∠F=∠G,∠FEC+∠ADC=180°,试判断AD∥BC吗?为什么?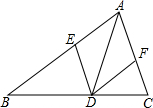 如图,已知AD平分∠BAC,要使△ADE≌△ADF,只需再添加一个条件就可以了,你选择的条件是AE=AF,理由是SAS.
如图,已知AD平分∠BAC,要使△ADE≌△ADF,只需再添加一个条件就可以了,你选择的条件是AE=AF,理由是SAS.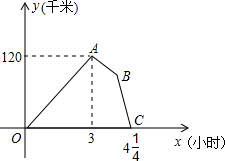 某物流公司的快递车和货车同时从甲地出发,以各自的速度沿平直公路匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度沿平直公路匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论: