题目内容
5.解方程组$\left\{\begin{array}{l}2{x^2}-3{y^2}=8\\ 2x-3\sqrt{3}y=-4\end{array}\right.$.分析 把2x-3$\sqrt{3}$y=-4变形,用含y的代数式表示x,代入另一个方程,解关于y的一元二次方程即可求出y值,把y的值代入二元一次方程求出x的值即可.
解答 解:$\left\{\begin{array}{l}{2{x}^{2}-3{y}^{3}=8①}\\{2x-3\sqrt{3}y=-4②}\end{array}\right.$,
由②得:x=$\frac{3\sqrt{3}y-4}{2}$③,
把③代入①得:2×($\frac{3\sqrt{3}y-4}{2}$)2-2y2=8,
解得:y1=0,y2=$\frac{8}{7}\sqrt{3}$,
把y1=0,y2=$\frac{8}{7}\sqrt{3}$代入③得,
x1=-2,x2=$\frac{22}{7}$.
所以方程组的解为:$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{22}{7}}\\{{y}_{2}=\frac{8}{7}\sqrt{3}}\end{array}\right.$.
点评 本题考查的是用代入法解二元二次方程组,解题的关键是掌握代入法解方程的步骤,因为含有二次根式,计算难度较大,所以解答过程中要仔细计算,避免因为计算失误导致结果错误.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
16.二次函数y=-x2+4与y轴的交点坐标是( )
| A. | (0,-2) | B. | (0,2) | C. | (0,-4) | D. | (0,4) |
20. 如图,AC垂直平分BD,垂足为E,连接AB,AD,BC,CD,下列结论不一定成立的是( )
如图,AC垂直平分BD,垂足为E,连接AB,AD,BC,CD,下列结论不一定成立的是( )
 如图,AC垂直平分BD,垂足为E,连接AB,AD,BC,CD,下列结论不一定成立的是( )
如图,AC垂直平分BD,垂足为E,连接AB,AD,BC,CD,下列结论不一定成立的是( )| A. | AB=AD | B. | AC平分∠BCD | C. | AB=BD | D. | △BEC≌△DEC |
 如图,平面直角坐标系中,直线AB分别交x轴正半轴于点A,交y轴正半轴于点B,且OA、OB(OA<OB)的长是方程x2-12x+32=0的两个根.
如图,平面直角坐标系中,直线AB分别交x轴正半轴于点A,交y轴正半轴于点B,且OA、OB(OA<OB)的长是方程x2-12x+32=0的两个根.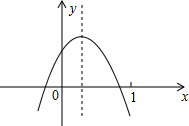 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:其中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:其中正确的有( ) 统计七年级若干名学生的跳高测试成绩,得到如图所示的频数分布直方图(每组数据含最小值,不含最大值).请回答下列问题:
统计七年级若干名学生的跳高测试成绩,得到如图所示的频数分布直方图(每组数据含最小值,不含最大值).请回答下列问题: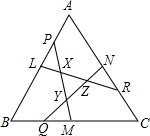 正△ABC,在边AB、BC、CA的正中间分别取点L、M、N,在边AL、BM、CN上分别取点P、Q、R,使LP=MQ=NR,当PM和RL、PM和QN、QN和RL的相交点分别是X、Y、Z时,使XY=XL,这时,△XYZ的面积是△ABC的几分之几?请写出思考过程.
正△ABC,在边AB、BC、CA的正中间分别取点L、M、N,在边AL、BM、CN上分别取点P、Q、R,使LP=MQ=NR,当PM和RL、PM和QN、QN和RL的相交点分别是X、Y、Z时,使XY=XL,这时,△XYZ的面积是△ABC的几分之几?请写出思考过程. 如图,在已知的△ABC中,按以下步骤作图:
如图,在已知的△ABC中,按以下步骤作图: