题目内容
19.已知a+$\frac{1}{a}$=$\frac{5}{2}$,则a-$\frac{1}{a}$=$±\frac{3}{2}$.分析 已知等式两边平方求出$;{a}^{2}+\frac{1}{{a}^{2}}$$;{a}^{2}+\frac{1}{{a}^{2}}$a2+$\frac{1}{{a}^{2}}$的值,原式变形后代入计算即可求出值.
解答 解:∵a+$\frac{1}{a}$=$\frac{5}{2}$,
两边同时平方得:$(a+\frac{1}{a})^{2}$=$(\frac{5}{2})^{2}$,
${a}^{2}+\frac{1}{{a}^{2}}$+2=$\frac{25}{4}$,
${a}^{2}+\frac{1}{{a}^{2}}$=$\frac{17}{4}$
∵$(a-\frac{1}{a})^{2}$=a2-2+$\frac{1}{{a}^{2}}$=$\frac{17}{4}$-2=$\frac{9}{4}$
∴$a-\frac{1}{a}$=$±\frac{3}{2}$
故答案为:$±\frac{3}{2}$.
点评 此题考查了分式的化简求值,属于常考题型,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列式子合并同类项正确的是( )
| A. | 3x+5y=8xy | B. | 15ab-15ba=0 | C. | 3y2-y2=3 | D. | 7x3-6x2=x |
11.用配方法解一元二次方程x2-6x+5=0,此方程可化为( )
| A. | (x-3)2=4 | B. | (x-3)2=14 | C. | (x+3)2=4 | D. | (x+3)2=14 |
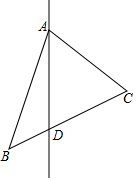 如图.已知△ABC.点D在BC边上.过点A作直线AD.
如图.已知△ABC.点D在BC边上.过点A作直线AD.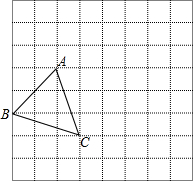 已知:如图在8×8的正方形网格中,每个小正方形的边长为1个单位长度,△ABC的每个顶点都在格点(每个小正方形的顶点)上,把△ABC向右平移4个单位,再向上平移1个单位得△A1B1C1;
已知:如图在8×8的正方形网格中,每个小正方形的边长为1个单位长度,△ABC的每个顶点都在格点(每个小正方形的顶点)上,把△ABC向右平移4个单位,再向上平移1个单位得△A1B1C1;